题目内容
在△ABC中,D为BC的中点,E为AC上任一点,BE交AD于O,某学生在研究这一问题时,发现了如下事实:
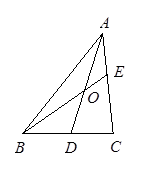
(1)当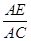 =
=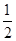 =
=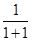 时,有
时,有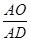 =
=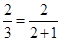 ;
;
(2)当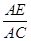 =
=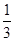 =
=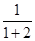 时,有
时,有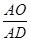 =
=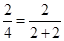 ;
;
(3)当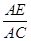 =
=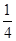 =
=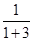 时,有
时,有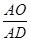 =
=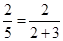 ;
;
1)当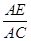 =
=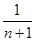 时,按照上述的结论,请你猜想
时,按照上述的结论,请你猜想
用n表示AO/AD的一般性结论(n为正整数);
2)若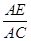 =
=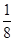 ,且AD=18,求AO.
,且AD=18,求AO.
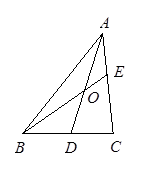
(1)当
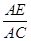 =
=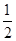 =
=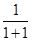 时,有
时,有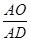 =
=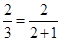 ;
;(2)当
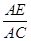 =
=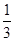 =
=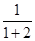 时,有
时,有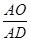 =
=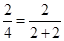 ;
;(3)当
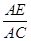 =
=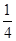 =
=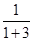 时,有
时,有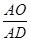 =
=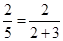 ;
;1)当
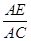 =
=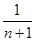 时,按照上述的结论,请你猜想
时,按照上述的结论,请你猜想用n表示AO/AD的一般性结论(n为正整数);
2)若
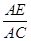 =
=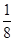 ,且AD=18,求AO.
,且AD=18,求AO.(1)AO/AD=2/(2+n)
(2)AO:AD=2:9,AD=18,∴AO=4
(2)AO:AD=2:9,AD=18,∴AO=4
①过D作DF∥BE,即求AE:AD,因为当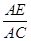 =
=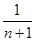 时,可以根据平行线分线段成比例,及线段相互间的关系即可得出.
时,可以根据平行线分线段成比例,及线段相互间的关系即可得出.
②利用①中方法得出AE:(AE+2EF)=1:8,进而得出AE:EF=2:7,以及AO/AD ="AE/AF=2/9"
得出答案即可.
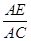 =
=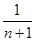 时,可以根据平行线分线段成比例,及线段相互间的关系即可得出.
时,可以根据平行线分线段成比例,及线段相互间的关系即可得出.②利用①中方法得出AE:(AE+2EF)=1:8,进而得出AE:EF=2:7,以及AO/AD ="AE/AF=2/9"
得出答案即可.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
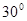 。则∠2= 度。
。则∠2= 度。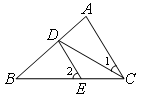
 ∥
∥ 的条件有( )个.
的条件有( )个.
 ; (2)
; (2) ;
;  ; (4)
; (4)  .
.


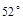 方向,C岛在B岛的北偏西
方向,C岛在B岛的北偏西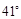 方向,则从 C岛看A、B两岛的视角
方向,则从 C岛看A、B两岛的视角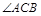 等于 ★ .
等于 ★ .