Question

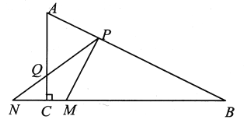
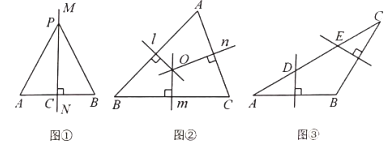
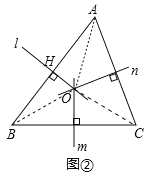
【题目】教材呈现：下图是华师版八年级上册数学教材第94页的部分内容．

请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程．

定理应用：

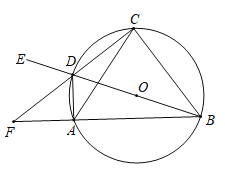
（1）如图②，在中，直线分别是边AB、BC、AC的垂直平分线．求证：直线交于点．

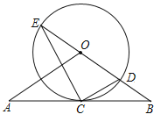
（2）如图③，在中，，边AB的垂直平分线交AC于点D、边BC的垂直平分线交AC于点E．若，，则DE的长为___________．

Answer 1

【答案】教材呈现：证明见解析；定理应用：（1）证明见解析；（2）6．

【解析】

教材呈现：如图①中，证明△PAC≌△PBC即可解决问题；

定理应用：（1）如图②中，连结AO、BO、CO．利用线段的垂直平分线的判定和性质解决问题即可；

（2）连接BD，BE，证明△BDE是等边三角形即可．

教材呈现：

∵MN⊥AB，

∴

又∵，

∴△PAC≌△PBC，

∴

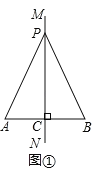
定理应用：

（1）连结AO、BO、CO．

设直线l、m交于点O．

∵直线l是边AB的垂直平分线，

∴

又∵直线m是边BC的垂直平分线，

∴，

∴，

∴点O在边AC的垂直平分线n上，

∴直线l、m、n交于点O．

（2）如图③中，连接BD，BE．

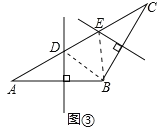
∵BA＝BC，∠ABC＝120°，

∴∠A＝∠C＝30°，

∵边AB的垂直平分线交AC于点D，边BC的垂直平分线交AC于点E，

∴DA＝DB，EB＝EC，

∴∠A＝∠DBA＝30°，∠C＝∠EBC＝30°，

∴∠BDE＝∠A+∠DBA＝60°，∠BED＝∠C+∠EBC＝60°，

∴△BDE是等边三角形，

∴AD＝BD＝DE＝BE＝EC，

∵AC＝18＝AD+DE+EC＝3DE，

∴DE＝6，

故答案为：6．