Question

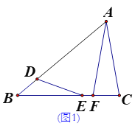
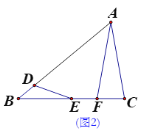
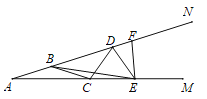
【题目】如图，若B、D、F在AN上，C、E在AM上，且AB=BC=CD=ED=EF，∠A=20°，则∠FEB= __________

Answer 1

【答案】70°

【解析】

先根据AB=BC=CD得到∠BCA=∠A，∠CDB=∠CBD，再通过三角形的外角性质得到△ECD是等边三角形，从而得到BC=CE，求出∠CEB的度数；由ED=EF得到∠EDF=∠EFD，再通过三角形的内角和公式和外角性质得到∠FEA的度数，∠FEA－∠CEB的值即为∠FEB的度数．

解：∵AB=BC，

∴ ∠BCA=∠A=20°，

∴∠CBD=∠BCA+∠A=20°+20°=40°．

又∵ BC=CD，

∴∠CDB=∠CBD=40°，

∴∠ECD=180°-∠BCA -∠BCD

=180°-20°-（180°-∠CBD-∠CDB）

=160°-（180°-40°-40°）

=60°

又∵CD=ED，∠ECD=60°，

∴△ECD是等边三角形，

∴BC=CE，∠CDE=60°，

∴∠CEB=∠BCA =×20°=10°，∠ADE=∠CDE+∠CDB=60°+40°=100°．

又∵ ED=EF，

∴∠EDF=∠EFD=180°-∠CEB=180°-100°=80°，

∴∠FEA=180°-∠A-∠EFD=180°-20°-80°=80°，

∴∠FEB=∠FEA-∠CEB=80°-10°=70°．

故答案为：70°．