题目内容
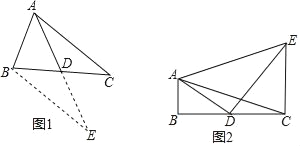
【题目】把两个全等的等腰直角三角板(直角边长为4)叠放在一起,且三角板EFG的直角顶点G位于三角板ABC的斜边中点处.现将三角板EFG绕G点按顺时针方向旋转α度(0°<α<90°)(如图1),四边形GKCH为两三角板的重叠部分.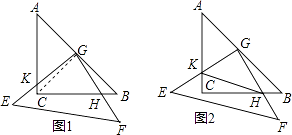
(1)猜想BH与CK有怎样的数量关系?并证明你的结论;
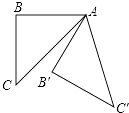
(2)连接HK(如图2),在上述旋转过程中,设BH=x,△GKH的面积为y,
①求y与x之间的函数关系式,并写出自变量x的取值范围;
②当△GKH的面积恰好等于△ABC面积的 ![]() ,求x.
,求x.
【答案】
(1)
解:BH=CK.
理由如下:∵点O是等腰直角三角板ABC斜边中点,
∴∠B=∠GCK=45°,BG=CG,
由旋转的性质,知∠BGH=∠CGK,
在△BGH和△CGK中,
 ,
,
∴△BGH≌△CGK(ASA),
∴BH=CK;
(2)
解:①∵△BGH≌△CGK,
∴S四边形CHGK=S△CGK+S△CGH=S△BGH+S△CGH=S△BCG= ![]() S△ABC=4,
S△ABC=4,
∴S△GKH=S四边形CHGK﹣S△KCH=4﹣ ![]() CH×CK,
CH×CK,
∴y= ![]() x2﹣2x+4(0<x<4),
x2﹣2x+4(0<x<4),
②当y= ![]() ×8=
×8= ![]() 时,即
时,即 ![]() x2﹣2x+4=
x2﹣2x+4= ![]() ,
,
∴x=1 或x=3.
∴当△GKH的面积恰好等于△ABC面积的 ![]() 时,BH=1 或BH=3.
时,BH=1 或BH=3.
【解析】(1)先由ASA证出△CGK≌△BGH,再根据全等三角形的性质得出BH=CK,根据全等得出四边形CKGH的面积等于三角形ACB面积一半;(2)①由(1)易得S四边形CHGK= ![]() S△ABC , 然后根据面积公式得出y=
S△ABC , 然后根据面积公式得出y= ![]() x2﹣2x+4;②根据△GKH的面积恰好等于△ABC面积的
x2﹣2x+4;②根据△GKH的面积恰好等于△ABC面积的 ![]() ,代入得出方程即可求得结果.
,代入得出方程即可求得结果.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目