题目内容
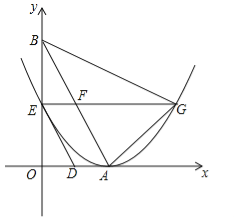
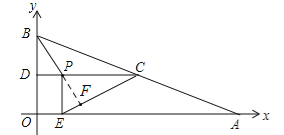
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为 .

【答案】(1,![]() ).
).
【解析】∵点A、B的坐标分别为(8,0),(0,![]() ),∴BO=
),∴BO=![]() ,AO=8.
,AO=8.
由CD⊥BO,C是AB的中点,可得BD=DO=![]() BO=
BO=![]() =PE,CD=
=PE,CD=![]() AO=4.设DP=a,则CP=4﹣a.
AO=4.设DP=a,则CP=4﹣a.
当BP所在直线与EC所在直线第一次垂直时,∠FCP=∠DBP.
又∵EP⊥CP,PD⊥BD,∴∠EPC=∠PDB=90°,∴△EPC∽△PDB,∴![]() ,即
,即![]() ,解得
,解得![]() =1,
=1,![]() =3(舍去),∴DP=1.又∵PE=
=3(舍去),∴DP=1.又∵PE=![]() ,∴P(1,
,∴P(1,![]() ).故答案为:(1,
).故答案为:(1,![]() ).
).

练习册系列答案
相关题目