Question

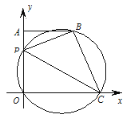
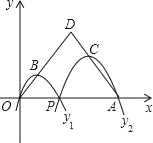
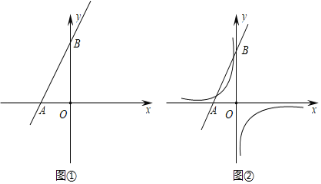
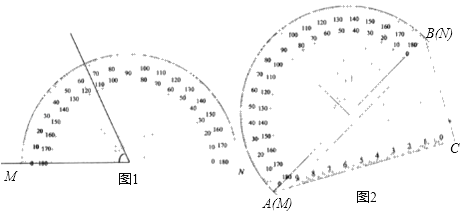
【题目】如图1，是用量角器一个角的操作示意图，量角器的读数从M点开始（即M点的读数为0），如图2，把这个量角器与一块30°（∠CAB＝30°）角的三角板拼在一起，三角板的斜边AB与量角器所在圆的直径MN重合，现有射线C绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB，在旋转过程中，射线CP与量角器的半圆弧交于E．连接BE．

（1）当射线CP经过AB的中点时，点E处的读数是　 　，此时△BCE的形状是　 　；

（2）设旋转x秒后，点E处的读数为y，求y与x的函数关系式；

（3）当CP旋转多少秒时，△BCE是等腰三角形？

Answer 1

【答案】（1）60°，直角三角形；（2）y＝4x（0≤x≤45）；（3）7.5秒或30秒

【解析】

（1）根据圆周角定理即可解决问题；

（2）如图2﹣2中，由题意∠ACE＝2x，∠AOE＝y，根据圆周角定理可知∠AOE＝2∠ACE，可得y＝2x（0≤x≤45）；

（3）分两种情形分别讨论求解即可；

解：（1）如图2﹣1中，

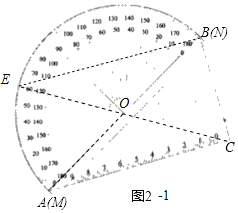
∵∠ACB＝90°，OA＝OB，

∴OA＝OB＝OC，

∴∠OCA＝∠OAC＝30°，

∴∠AOE＝60°，

∴点E处的读数是60°，

∵∠E＝∠BAC＝30°，OE＝OB，

∴∠OBE＝∠E＝30°，

∴∠EBC＝∠OBE+∠ABC＝90°，

∴△EBC是直角三角形；

故答案为60°，直角三角形；

（2）如图2﹣2中，

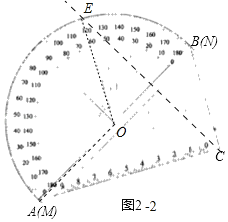
∵∠ACE＝2x，∠AOE＝y，

∵∠AOE＝2∠ACE，

∴y＝4x（0≤x≤45）．

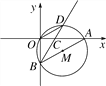
（3）①如图2﹣3中，当EB＝EC时，EO垂直平分线段BC，

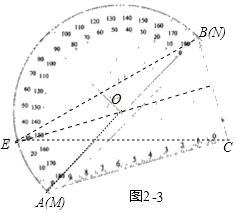
∵AC⊥BC，

∵EO∥AC，

∴∠AOE＝∠BAC＝30°，

∴∠ECA＝∠AOE＝15°，

∴x＝7.5．

②若2﹣4中，当BE＝BC时，

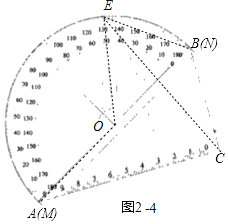
易知∠BEC＝∠BAC＝∠BCE＝30°，

∴∠OBE＝∠OBC＝60°，

∵OE＝OB，

∴△OBE是等边三角形，

∴∠BOE＝60°，

∴∠AOB＝120°，

∴∠ACE＝∠ACB＝60°，

∴x＝30，

综上所述，当CP旋转7.5秒或30秒时，△BCE是等腰三角形；