题目内容
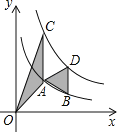
【题目】如图，反比例函数y＝
（x＜0）的图象过格点（网格线的交点）P．
（1）求反比例函数的解析式；
（2）在图中用直尺和2B铅笔画出两个三角形（不写画法），要求每个三角形均需满足下列两个条件：
①三个顶点均在格点上，且其中两个顶点分别是点O，点P；
②三角形的面积等于|k|的值．
【答案】（1）
；（2）详见解析
【解析】
（1）利用待定系数法即可求得；
（2）根据三角形满足的两个条件画出符合要求的两个三角形即可．
解：（1）∵反比例函数y＝
（x＜0）的图象过格点P，
由图象易知P点坐标是（﹣2，1），
∴将P（﹣2，1）代入y＝得，k＝﹣2×1＝﹣2，
∴反比例函数的解析式为；
（2）如图所示：△APO、△BPO即为所求作的图形；
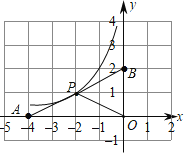
第三个点可以是（﹣4，0），（﹣2，﹣1），（4，0），（﹣2，3），（﹣6，1），（2，1），（0，2），（0，﹣2）．
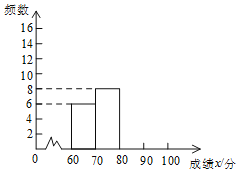
【题目】第十二届校园艺术节正在如火如荼的进行，我校九年级组织1500名学生参加了一次“湘一情校园知识”大赛．赛后发现所有参赛学生的成绩均不低于60分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩作为样本，成绩如下：
90，92，81，82，78，95，86，88，72，66，62，68，89，86，93，97，100，73，76，80，77，81，86，89，82，85，71，68，74，98，90，97，100，84，87，73，65，92，96，60．
对上述成绩进行了整理，得到下列不完整的统计图表：
成绩x/分 | 频数 | 频率 |
60≤x＜70 | 6 | 0.15 |
70≤x＜80 | 8 | 0.2 |
80≤x＜90 | a | b |
90≤x≤100 | c | d |
请根据所给信息，解答下列问题：
（1）a＝ ，b＝ ，c＝ ，d＝ ；
（2）请补全频数分布直方图；
（3）若成绩在90分以上（包括90分）的为“优”等，请你估计参加这次比赛的1500名学生中成绩“优”等的约有多少人？
