题目内容
【题目】已知：在Rt△ABC中，∠ACB＝90°，AC＝BC，点D在直线AB上，连接CD，并把CD绕点C逆时针旋转90°到CE．
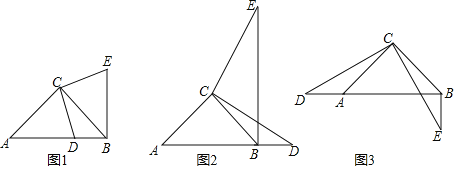
（1）如图1，点D在AB边上，线段BD、BE、CD的数量关系为 ．
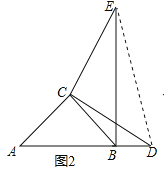
（2）如图2，点D在点B右侧，请猜想线段BD、BE、CD的数量关系，并证明你的结论．
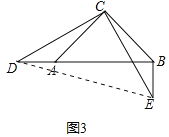
（3）如图3，点D在点A左侧，BC＝
，AD＝BE＝1，请直接写出线段EC的长．
【答案】（1）结论：BE2+BD2＝2CD2（2）结论：BE2+BD2＝2CD2（3）
【解析】
（1）如图1中，连接DE，易证△ACD≌△BCE（SAS），得到AD＝BE，∠CAD＝∠CBE，得到∠A＝∠CBA＝45°，则∠ABE＝90°，有DE2＝BD2+BE2，DE＝
CD，得到BE2+BD2＝2CD2．
（2）整体思路如（1）先证△ACD≌△BCE，然后找出DE2＝BD2+BE2，利用DE＝CD，即可得证
（3）如图3中，连接DE．先求出BD，然后利用前两问结论直接代入计算即可
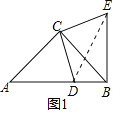
解：（1）结论：BE2+BD2＝2CD2．
理由：如图1中，连接DE．
∵∠ACB＝∠DCE＝90°，
∴∠ACD＝∠BCE，
∵CA＝CB，CD＝CE，
∴△ACD≌△BCE（SAS），
∴AD＝BE，∠CAD＝∠CBE，
∵CA＝CB，∠ACB＝90°，
∴∠A＝∠CBA＝45°，
∴∠CBE＝∠A＝45°，
∴∠ABE＝90°，
∴DE2＝BD2＝BE2，
∵DE＝CD，
∴BE2+BD2＝2CD2．
（2）结论：BE2+BD2＝2CD2．
理由：如图2中，连接DE．
∵∠ACB＝∠DCE＝90°，
∴∠ACD＝∠BCE，
∵CA＝CB，CD＝CE，
∴△ACD≌△BCE（SAS），
∴AD＝BE，∠CAD＝∠CBE，
∵CA＝CB，∠ACB＝90°，
∴∠A＝∠CBA＝45°，
∴∠CBE＝∠A＝45°，
∴∠ABE＝∠EBD＝90°，
∴DE2＝BD2+BE2，
∵DE＝CD，
∴BE2+BD2＝2CD2．
（3）如图3中，连接DE．
∵AC＝BC＝，∠ACB＝90°，
∴AB＝BC＝2，
∴AD＝BE＝1，
∴BD＝3，
由（2）可知：BD2+BE2＝2EC2，
∴9+1＝2EC2，
∴EC＝．
