题目内容
24、如图，M是Rt△ABC斜边AB上的中点，D是边BC延长线上一点，∠B=2∠D，AB=16cm，求线段CD的长．分析：根据直角三角形斜边上中线得到BM=CM，推出∠B=∠MCB，根据三角形外角性质求出∠D=∠DMC，推出DC=CM，即可求出答案．
解答：解：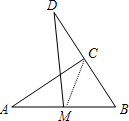
连接CM，
∵∠ACB=90°，M为AB的中点，
∴CM=BM=AM=8cm，
∴∠B=∠MCB=2∠D，
∵∠MCB=∠D+∠DMC，
∴∠D=∠DMC，
∴DC=CM=8cm．
答：线段CD的长是8cm．
连接CM，∵∠ACB=90°，M为AB的中点，
∴CM=BM=AM=8cm，
∴∠B=∠MCB=2∠D，
∵∠MCB=∠D+∠DMC，
∴∠D=∠DMC，
∴DC=CM=8cm．
答：线段CD的长是8cm．
点评：本题主要考查对直角三角形斜边上的中线，三角形的外角性质，等腰三角形的性质和判定等知识点的理解和掌握，能推出DC=CM是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
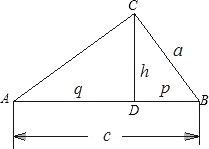已知：如图，CD是Rt△ABC的斜边AB上的高，且BC=a，AB=c，CD=h，AD=q，DB=p．求证：h2=p•q，a2=p•c．
如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，点P是圆外一点，PA切⊙O于点A，且PA=PB．
如图，△ABC是Rt△，∠CAB=30°，BC=1，以AB、BC、AC为边分别作3个等边△ABF，△BCE，△ACD．过F作MF垂直DA的延长线于点M，连接并延长DE交MF的延长线于点N．那么tan∠N=
如图，⊙O是Rt△ABC的外接圆，∠BAC的平分线与⊙O相交于点D，过点D作⊙O的切线EF，与AC的延长线交于点E，与AB的延长线交于点F．
如图，CD是Rt△ABC斜边AB上的高，若AB=5，AC=4，则BD=