题目内容
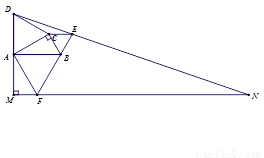
 如图,△ABC是Rt△,∠CAB=30°,BC=1,以AB、BC、AC为边分别作3个等边△ABF,△BCE,△ACD.过F作MF垂直DA的延长线于点M,连接并延长DE交MF的延长线于点N.那么tan∠N=
如图,△ABC是Rt△,∠CAB=30°,BC=1,以AB、BC、AC为边分别作3个等边△ABF,△BCE,△ACD.过F作MF垂直DA的延长线于点M,连接并延长DE交MF的延长线于点N.那么tan∠N=
| ||
| 5 |
| ||
| 5 |
分析:作EG⊥MN于点G,在直角△ABC中,利用三角函数即可求得AB、AC的长度,从而求得DM、EF的长,在直角△EFG中,利用三角函数求得FG的长,EG的长度,然后利用△DMN∽△EGN,相似三角形的对应边的比相等,即可求得MN的长,然后利用正切函数的定义即可求解.
解答: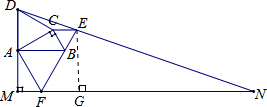 解:作EG⊥MN于点G.
解:作EG⊥MN于点G.
∵在直角△ABC中,BC=1,∠CAB=30°,
∴AB=2,AC=
,
∵△ABF,△BCE,△ACD是等边三角形,
∴AD=AC=
,AB=BF=AF=2,BE=BC=1,
∵在直角△AMF中,∠MAF=30°,AF=AB=2,
∴AM=
,MF=1,
∴DM=AD+AM=
+
=2
,EF=BE+BF=1+2=3,
又∵直角△EFG中,∠FEG=30°,
∴FG=
EF=
,EG=
,
∴MG=1+
=
,
∵EG∥DM,
∴△DMN∽△EGN,
∴
=
,设GN=x,
∴
=
,
解得:x=
,则MN=
+
=10,
∴tanN=
=
=
.
故答案是:
.
 解:作EG⊥MN于点G.
解:作EG⊥MN于点G.∵在直角△ABC中,BC=1,∠CAB=30°,
∴AB=2,AC=
| 3 |
∵△ABF,△BCE,△ACD是等边三角形,
∴AD=AC=
| 3 |
∵在直角△AMF中,∠MAF=30°,AF=AB=2,
∴AM=
| 3 |
∴DM=AD+AM=
| 3 |
| 3 |
| 3 |
又∵直角△EFG中,∠FEG=30°,
∴FG=
| 1 |
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
∴MG=1+
| 3 |
| 2 |
| 5 |
| 2 |
∵EG∥DM,
∴△DMN∽△EGN,
∴
| EG |
| DM |
| GN |
| MN |
∴
| ||||
2
|
| x | ||
x+
|
解得:x=
| 15 |
| 2 |
| 15 |
| 2 |
| 5 |
| 2 |
∴tanN=
| DM |
| MN |
2
| ||
| 10 |
| ||
| 5 |
故答案是:
| ||
| 5 |
点评:本题考查了三角函数的定义,以及解直角三角形的方法,相似三角形的性质,正确求得MN的长度是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
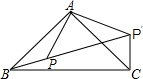 如图,△ABC是Rt△,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于
如图,△ABC是Rt△,BC是斜边,P是三角形内一点,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′的长等于