题目内容
 如图,⊙O是Rt△ABC的外接圆,∠BAC的平分线与⊙O相交于点D,过点D作⊙O的切线EF,与AC的延长线交于点E,与AB的延长线交于点F.
如图,⊙O是Rt△ABC的外接圆,∠BAC的平分线与⊙O相交于点D,过点D作⊙O的切线EF,与AC的延长线交于点E,与AB的延长线交于点F.(1)试判断EF与BC的位置关系,并说明理由;
(2)若FD=6,AF=9,求⊙O的半径.
分析:(1)连结OD,就可以由条件得出OD∥AE,就可以得出∠ODF=∠AEF,由切线的性质可以得出∠ODF=90°,进而有∠E=90°,由∠ACB=90°就可以得出∠E=∠ACB,就有BC∥EF;
(2)根据切割线定理就可以得出BF的值,就可以得出AB的值而得出半径.
(2)根据切割线定理就可以得出BF的值,就可以得出AB的值而得出半径.
解答:解:(1)BC∥EF,理由如下:
连结OD.
∵EF是⊙O的切线交⊙O于点D,
∴OD⊥EF,∠ODA=∠OAD.
∴∠ODF=90°.
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∴∠ODA=∠EAD,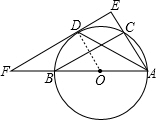
∴OD∥AE,
∴∠ODF=∠E=90°.
∵AB是⊙O的直径,
∴∠ACB=90°
∴∠ACB=∠E,
∴BC∥EF;
(2)∵EF是⊙O的切线,
∴DF2=BF•AF.
∵FD=6,AF=9,
∴36=9BF,
∴BF=4,
∴AB=5,
∴OB=2.5
答:⊙O的半径为2.5.
连结OD.
∵EF是⊙O的切线交⊙O于点D,
∴OD⊥EF,∠ODA=∠OAD.
∴∠ODF=90°.
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∴∠ODA=∠EAD,

∴OD∥AE,
∴∠ODF=∠E=90°.
∵AB是⊙O的直径,
∴∠ACB=90°
∴∠ACB=∠E,
∴BC∥EF;
(2)∵EF是⊙O的切线,
∴DF2=BF•AF.
∵FD=6,AF=9,
∴36=9BF,
∴BF=4,
∴AB=5,
∴OB=2.5
答:⊙O的半径为2.5.
点评:本题考查了平行线的性质及判定的运用,切线的性质的运用,角平分线的性质的运用,切割线定理的运用,解答时运用好切线的性质求解是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 7、如图,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有( )
7、如图,CD是Rt△ABC斜边上的高,则图中相似三角形的对数有( ) 如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F.
如图,CD是Rt△ABC斜边上的高,E为AC的中点,ED交CB的延长线于F. 24、如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长.
24、如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16cm,求线段CD的长. (2013•顺义区二模)已知:如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(2013•顺义区二模)已知:如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB. 如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5
如图,BD是Rt△DAB和Rt△DCB的公共边,∠A、∠C是直角,∠ADC=60°,BC=2cm,AD=5