题目内容
 如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是
如图,a∥b,∠1=105°,∠2=140°,则∠3的度数是
- A.75°
- B.65°
- C.55°
- D.50°
B
分析:如图作出两直线的交点,由a∥b可以推出∠1+∠4=180°,然后可以求出∠4=75°.再根据三角形的外角等于不相邻的两个内角的和可以求出∠3.
解答: 解:如图作出两直线的交点,
解:如图作出两直线的交点,
∵a∥b,
则∠1+∠4=180°,
∴∠4=75°,
根据三角形的外角等于不相邻的两个内角的和得到∠2=∠3+∠4,
则∠3=65°.
故选B.
点评:本题主要运用了平行线的性质定理,以及三角形的外角等于不相邻的两个内角的和.
分析:如图作出两直线的交点,由a∥b可以推出∠1+∠4=180°,然后可以求出∠4=75°.再根据三角形的外角等于不相邻的两个内角的和可以求出∠3.
解答:
 解:如图作出两直线的交点,
解:如图作出两直线的交点,∵a∥b,
则∠1+∠4=180°,
∴∠4=75°,
根据三角形的外角等于不相邻的两个内角的和得到∠2=∠3+∠4,
则∠3=65°.
故选B.
点评:本题主要运用了平行线的性质定理,以及三角形的外角等于不相邻的两个内角的和.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
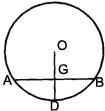 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=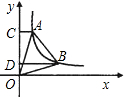 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

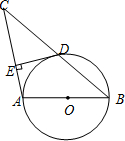 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.