题目内容
【题目】如图,有一直角三角形![]() ,一条线段
,一条线段![]() 两点分别在
两点分别在![]() 上和过
上和过![]() 点且垂直于
点且垂直于![]() 的射线
的射线![]() 上运动,当
上运动,当![]() 点运动到
点运动到![]() 上什么位置时
上什么位置时![]() 才能和以
才能和以![]() 为顶点的三角形全等.
为顶点的三角形全等.
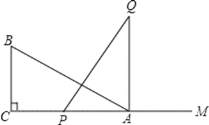
【答案】当P运动到距点A5cm或10cm时,△ABC和△APQ全等.
【解析】
本题要分情况讨论:①Rt△APQ≌Rt△CBA,此时AP=BC=5cm,可据此求出P点的位置;②Rt△QAP≌Rt△BCA,此时AP=AC,P、C重合.
根据三角形全等的判定方法HL可知:
①当P运动到AP=BC时,
∵∠C=∠QAP=90°,
在Rt△ABC与Rt△QPA中,
![]() ,
,
∴Rt△ABC≌Rt△QPA(HL),
即AP=BC=5cm;
②当P运动到与C点重合时,AP=AC,
在Rt△ABC与Rt△QPA中,
![]() ,
,
∴Rt△QAP≌Rt△BCA(HL),
即AP=AC=10cm,
∴当点P与点C重合时,△ABC才能和△APQ全等.
综上所述,当P运动5cm或10cm时,△ABC和△APQ全等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目