题目内容
【题目】 已知,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
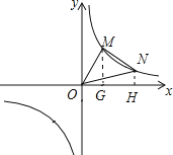
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
【答案】(1)y=-x-3;(2)m2+n2=13;(3)S△MON=3
【解析】
(1)先求得A、B的坐标,然后根据待定系数法求解即可;
(2)由点P与点Q关于x轴对称可得点Q的坐标,然后根据图象上点的坐标特征可求得mn=2,n=m+3,然后代入所求式子整理化简即得结果;
(3)如图,过M作MG⊥x轴于G,过N作NH⊥x轴于H,根据反比例函数系数k的几何意义,利用S△MON=S梯形MNHG+S△MOG-S△NOH=S梯形MNHG即可求得结果.
解:(1)∵反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1,
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1,
∴A(﹣1,﹣2),B(﹣2,﹣1),
设一次函数的表达式为y=kx+b,把A(﹣1,﹣2),B(﹣2,﹣1)代入,得:
![]() ,解得
,解得![]() ,
,
∴这个一次函数的表达式为y=﹣x﹣3;
(2)∵点P(m,n)与点Q关于x轴对称,∴Q(m,-n),
∵点P(m,n)在反比例函数图象上,∴mn=2,
∵点Q恰好落在一次函数的图象上,∴﹣n=﹣m﹣3,即n=m+3,
∴m(m+3)=2,∴m2+3m=2,
∴m2+n2=m2+(m+3)2=2m2+6m+9=2(m2+3m)+9=2×2+9=13;
(3)如图,过M作MG⊥x轴于G,过N作NH⊥x轴于H,
∵M(x1,y1),N(x2,y2)是反比例函数y=![]() 在第一象限图象上的两点,
在第一象限图象上的两点,
∴S△MOG=S△NOH=![]() =1,
=1,
∵x2-x1=2,y1+y2=3,
∴S△MON=S梯形MNHG+S△MOG-S△NOH=S梯形MNHG=![]() =
=![]() =3.
=3.