题目内容
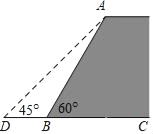
【题目】如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=45°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】应将堤坝底端向外拓宽(BD)8.8米.
【解析】
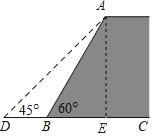
过A点作AE⊥CD于E,在Rt△ABE中,根据∠ABC=60°,AB=24米,求出AE的长度,然后在Rt△ADE中求出DE的长度,继而可求得BD的长度
过点A作AE⊥BC,
∵AB=24米,∠ABC=60°,
∴AE=ABsin60°=12![]() 米,
米,
BE=ABcos60°=12米,
∵AE=12![]() 米,∠ADB=45°,
米,∠ADB=45°,
∴DE=12![]() 米,
米,
∴BD=12![]() ﹣12=12(
﹣12=12(![]() ﹣1)≈8.8米.
﹣1)≈8.8米.
答:应将堤坝底端向外拓宽(BD)8.8米.

练习册系列答案
相关题目