题目内容
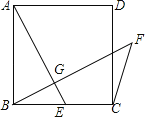
【题目】如图，在正方形ABCD中，F为DC的中点，E为BC 上一点，BC=4CE．求证：AF⊥FE．
【答案】证明过程见解析
【解析】
试题分析：连接AE，设正方形的边长为4a，分别根据Rt△ADF，Rt△ABE和Rt△ECF的勾股定理求出
,
和
的值，然后根据勾股定理的逆定理得出垂直.
试题解析：连接AE，设正方形的边长为4a．
在Rt△ADF中， AD=4a，DF=2a， 据勾股定理得，AF2=AD2+DF2， 解得：AF2=20a2．
在Rt△ABE中， AB=4a，BE=3a， 据勾股定理得，AE2=AB2+BE2， 解得：AE2=25a2．
在Rt△ECF中， FC=2a，CE=a， 据勾股定理得，EF2=CF2+CE2， 解得：EF2=5a2．
∴AE2=AF2+EF2， ∴AF⊥FE．
练习册系列答案
名校课堂系列答案
相关题目
