题目内容
【题目】如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°求证:AG=FG.
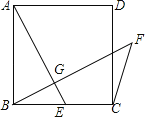
【答案】见解析
【解析】
试题分析:过C点作CH⊥BF于H点,根据已知条件可证明△AGB≌△BHC,所以AG=BH,BG=CH,又因为BH=BG+GH,所以可得BH=HF+GH=FG,进而证明AG=FG.
证明:过C点作CH⊥BF于H点,
∵∠CFB=45°,
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
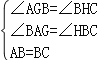 ,
,
∴△AGB≌△BHC,
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG.

练习册系列答案
相关题目