题目内容
【题目】已知AB∥CD,解决下列问题:
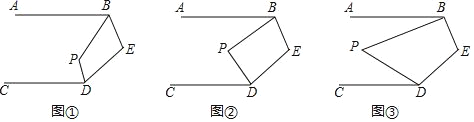
(1)如图①,BP、DP分别平分∠ABE、∠CDE,若∠E=100°,求∠P的度数.
(2)如图②,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,试写出∠P与∠E的数量关系并说明理由.
∠CDE,试写出∠P与∠E的数量关系并说明理由.
(3)如图③,若∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
∠CDE,设∠E=m°,求∠P的度数(直接用含n、m的代数式表示,不需说明理由).
【答案】(1)∠P=130°;(2)3∠P+∠BED=360°;(3)∠P=![]() .
.
【解析】
(1)过E作EF∥AB,依据平行线的性质,即可得到∠ABE+∠BED+∠CDE=360°,再根据∠BED=100°,BP、DP分别平分∠ABE、∠CDE,即可得到∠P的度数.
(2)过E作EF∥AB,依据平行线的性质,即可得到∠ABE+∠CDE=360°﹣∠BED,再根据∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,即可得到∠PBE+∠PDE=
∠CDE,即可得到∠PBE+∠PDE=![]() (∠ABE+∠CDE)=240°﹣
(∠ABE+∠CDE)=240°﹣![]() ∠BED,再根据四边形内角和得出∠P与∠E的数量关系;
∠BED,再根据四边形内角和得出∠P与∠E的数量关系;
(3)利用平行线的性质可得∠ABE+∠CDE=360°﹣∠BED=360°﹣m°,再根据∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,即可得到∠PBE+∠PDE=
∠CDE,即可得到∠PBE+∠PDE=![]() (∠ABE+∠CDE)=
(∠ABE+∠CDE)=![]() (360°﹣m°),再根据四边形PDEB内角和,即可得到∠P=360°﹣
(360°﹣m°),再根据四边形PDEB内角和,即可得到∠P=360°﹣![]() (360°﹣m°)﹣m°=
(360°﹣m°)﹣m°=![]() .
.
解:(1)如图①,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠ABE+∠BEF=180°,∠CDE+∠DEF=180°,
∴∠ABE+∠BED+∠CDE=360°,
又∵∠BED=100°,
∴∠ABE+∠CDE=360°﹣100°=260°,
又∵BP、DP分别平分∠ABE、∠CDE,
∴∠PBE+∠PDE=![]() (∠ABE+∠CDE)=
(∠ABE+∠CDE)=![]() ×260°=130°,
×260°=130°,
∴∠P=360°﹣130°﹣100°=130°;
(2)3∠P+∠BED=360°;
如图②,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠ABE+∠BEF=180°,∠CDE+∠DEF=180°,
∴∠ABE+∠BED+∠CDE=360°,
∴∠ABE+∠CDE=360°﹣∠BED,
又∵∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,
∠CDE,
∴∠PBE+∠PDE=![]() (∠ABE+∠CDE)=
(∠ABE+∠CDE)=![]() ×(360°﹣∠BED)=240°﹣
×(360°﹣∠BED)=240°﹣![]() ∠BED,
∠BED,
∴∠P=360°﹣∠BED﹣(240°﹣![]() ∠BED)=120°﹣
∠BED)=120°﹣![]() ∠BED,
∠BED,
即3∠P+∠BED=360°;
(3)∠P=![]() .
.
如图③,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
同理可得,∠ABE+∠CDE=360°﹣∠BED=360°﹣m°,
又∵∠ABP=![]() ∠ABE,∠CDP=
∠ABE,∠CDP=![]() ∠CDE,
∠CDE,
∴∠PBE+∠PDE=![]() (∠ABE+∠CDE)=
(∠ABE+∠CDE)=![]() (360°﹣m°),
(360°﹣m°),
∴四边形PDEB中,∠P=360°﹣![]() (360°﹣m°)﹣m°=
(360°﹣m°)﹣m°=![]() .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案

