题目内容
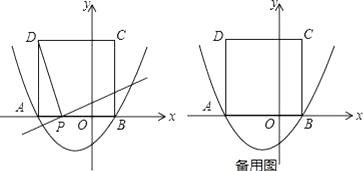
【题目】如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.

(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:在y=-x+3中,令y=0,得x=3;令x=0,得y=3,
∴B(3,0),C(0,3)
∵抛物线y=-x2+bx+c经过B、C两点
∴ ![]()
解得 ![]()
∴抛物线的函数表达式为y=-x2+2x+3
(2)解:∵P(m,0),PD∥y轴交直线BC于D,交抛物线于E
∴D(m,-m+3),E(m,-m2+2m+3)
∴DE=-m2+2m+3-(-m+3)=-m2+3m=-(m- ![]() )2+
)2+ ![]()
∴当m= ![]() 时,DE有最大值
时,DE有最大值 ![]() ,
,
由题意可知四边形DEFG为矩形
∵OB=OC=3,
∴∠DBP=∠BDP=∠EDF=∠EFD=45°
∴DE=EF∴四边形DEFG为正方形
∴S=DE2
∴当m= ![]() 时,S有最大值
时,S有最大值 ![]() ;
;
(3)解:如图所示,
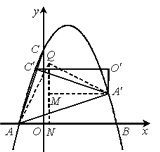
有两种情况:
①当点A′、C′落在抛物线上时
由O′A′=OA=1,O′C′=OC=3
设A′(a,-a2+2a+3),则C′(a-3,-a2+2a+4)
∴-a2+2a+4=-(a-3)2+2(a-3)+3
解得a= ![]() ,∴A′(
,∴A′( ![]() ,
, ![]() )
)
作QN⊥x轴于N,A′M⊥QN于M,连接QA、QA′
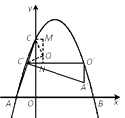
则∠AQA′=90°,可证△QAN≌△A′QM
设Q(x,y),则QM=AN=x+1
A′M=QN=y=x+1+ ![]() =
= ![]() -x
-x
解得x= ![]() ,y=
,y= ![]()
∴Q1( ![]() ,
, ![]() )
)
②当点O′、C′落在抛物线上时
则O′、C′两点关于抛物线的对称轴对称,易知抛物线的对称轴为直线x=1,
由O′C′=OC=3,可知C′(- ![]() ,
, ![]() ),
),
作QN⊥O′C′于N,CM⊥QN于M,连接QC、QC′
则∠CQC′=90°,
可证△CQM≌△QC′N,
设Q(x,y),则QM=C′N=x+ ![]()
CM=QN=y- ![]() =x=3-(x+
=x=3-(x+ ![]() )-
)- ![]()
解得x= ![]() ,y=
,y= ![]()
∴Q2( ![]() ,
, ![]() )
)
综上所述,存在符合条件的点Q,点Q的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )
)
【解析】(1) 根据直线BC的解析式求出点B、C的坐标,再将点B、C的坐标代入二次函数解析式求出b、c的值,即可得出抛物线的函数解析式。
(2)设点P的坐标为(m,0),根据PD∥y轴,点D和点E分别在直线BC上和抛物线上,因此可表示出点D、E的坐标,再求出DE与m的函数解析式,求出其顶点坐标,得出DE取最大值时m的值,再根据矩形的性质及点B、C的坐标,得出OB=OC、DE=EF,就可证明四边形DEFG为正方形,根据正方形的面积公式,求出s的最大值即可。
(3)此题分两种情况:①当点A′、C′落在抛物线上时,根据旋转的性质 得出O′A′=OA=1,O′C′=OC=3,设点A′,表示出C′的坐标,根据x=a-3时,y=-a2+2a+4,建立方程求解即可表示出Q1的坐标;②当点O′、C′落在抛物线上时,则O′、C′两点关于抛物线的对称轴对称,易知抛物线的对称轴为直线x=1,得出C′的坐标,作QN⊥O′C′于N,CM⊥QN于M,连接QC、QC′,证明△CQM≌△QC′N,根据CM=QN建立方程,从而得到Q2的坐标,得出结论即可。
【考点精析】利用二次函数的最值和旋转的性质对题目进行判断即可得到答案,需要熟知如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

 初中暑期衔接系列答案
初中暑期衔接系列答案