题目内容
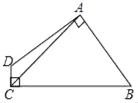
【题目】如图(1),在![]() 中,
中,![]() .若将
.若将![]() 绕点
绕点![]() 顺时针旋转至Δ
顺时针旋转至Δ![]() ,使射线
,使射线![]() 与射线
与射线![]() 相交于点
相交于点![]() (不与
(不与![]() 、
、![]() 重合).
重合).
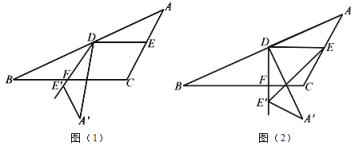
(1)如图(1),若![]() ,则
,则![]() ;
;
(2)如图(2),连结![]() ,若
,若![]() ,试求出
,试求出![]() 的度数;
的度数;
(3)请探究![]() 与
与![]() 之间所满足的数量关系,并加以证明.
之间所满足的数量关系,并加以证明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)由两直线平行内错角相等即可得到答案;
(2)根据旋转前后线段和角相等及![]() 可得到△
可得到△![]() 为等腰直角三角形,从而得到
为等腰直角三角形,从而得到![]() 的度数;
的度数;
(3)分两种情况讨论:①射线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,②射线
,②射线![]() 与
与![]() 延长线相交于点
延长线相交于点![]() ,通过平行线的性质和题中的角度关系即可得到答案.
,通过平行线的性质和题中的角度关系即可得到答案.
解:(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
故答案为![]() ;
;
(2)由旋转可知![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴△![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ;
;
(3)![]() 或
或![]() ,
,
①如图(2),射线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,
,

由旋转可知![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
由于![]() ,
,![]() ,
,
∴![]() ,
,
②如下图,射线![]() 与
与![]() 延长线相交于点
延长线相交于点![]() ,
,

由旋转可知![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,
故答案为:![]() 或
或![]() .
.

练习册系列答案
相关题目