题目内容
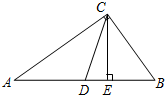
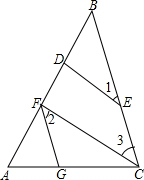
如图,在△ABC中,CF⊥AB于F,ED⊥AB于D,∠1=∠2.
(1)求证:FG∥BC;
(2)若∠A=60°,∠AFG=40°,求∠ACB的度数.

(1)求证:FG∥BC;
(2)若∠A=60°,∠AFG=40°,求∠ACB的度数.

(1)证明:如图,∵CF⊥AB,ED⊥AB,
∴DE∥FC,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴FG∥BC;
(2)如图,在△AFG中,∠A=60°,∠AFG=40°,
∴∠AGF=180°-∠A-∠AFG=100°.
又由(1)知,FG∥BC,
∴∠ACB=∠AGF=80°,即∠ACB的度数是80°.
∴DE∥FC,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴FG∥BC;
(2)如图,在△AFG中,∠A=60°,∠AFG=40°,
∴∠AGF=180°-∠A-∠AFG=100°.
又由(1)知,FG∥BC,
∴∠ACB=∠AGF=80°,即∠ACB的度数是80°.


练习册系列答案
相关题目