题目内容
【题目】如图,![]() 中,
中,![]() ,高
,高![]() 、
、![]() 相交于点
相交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,则图中全等的直角三角形共有( )
,则图中全等的直角三角形共有( )
A.4对B.5对C.![]() 对D.7对
对D.7对
【答案】C
【解析】
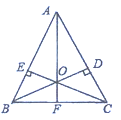
首先根据等腰三角形得到∠ABC=∠ACB,证明△BCE≌△CBD,得到BE=CD,可证△OBE≌△OCD,同时得到AE=AD,再证明△ABD≌△ACF,得到EO=DO,证明△OAE≌△OAD得到∠BAF=∠CAF ,证得△ABF≌△ACF,△OBF≌△OCF,故可求解.
∵![]() ,∴∠ABC=∠ACB
,∴∠ABC=∠ACB
∵高![]() 、
、![]() 相交于点
相交于点![]() ,∴∠BEC=∠CDB,又BC=CB,
,∴∠BEC=∠CDB,又BC=CB,
∴△BCE≌△CBD(AAS),
∴BE=CD,∴AE=AD
∴△ABD≌△ACF(SAS),
又∠BOE=∠COD,∴△OBE≌△OCD(AAS),∴EO=DO
∴△OAE≌△OAD(SSS)
∴∠BAF=∠CAF ,
∴△ABF≌△ACF(SAS),
∴BF=CF
∴△OBF≌△OCF(SSS)
故有6对全等的直角三角形
故选C

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目