Question

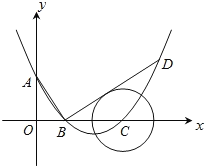
【题目】如图,在平面直角坐标系中,顶点为(4,1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).

（1）求此抛物线的解析式；

（2）已知点P是抛物线上的一个动点，且位于A，C两点之间，问：当点P运动到什么位置时，△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积；

（3）过点B作线段AB的垂线交抛物线于点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与有怎样的位置关系，并给出证明.

Answer 1

【答案】（1） （2）P点的坐标为；（3）相交．证明解解析.

【解析】分析：（1）已知抛物线的顶点坐标，可用顶点式设抛物线的解析式，然后将A点坐标代入其中，即可求出此二次函数的解析式；
（2）过P作y轴的平行线，交AC于Q；易求得直线AC的解析式，可设出P点的坐标，进而可表示出P、Q的纵坐标，也就得出了PQ的长；然后根据三角形面积的计算方法，可得出关于的面积与P点横坐标的函数关系式，根据所得函数的性质即可求出的最大面积及对应的P点坐标．

（3）根据抛物线的解析式，易求得对称轴的方程及B、C的坐标，分别求出直线AB、BD、CE的解析式，再求出CE的长，与到抛物线的对称轴的距离相比较即可；

详解：（1）设抛物线为

∵抛物线经过点A（0，3），

∴

∴抛物线为

（2）如图，过点P作平行于y轴的直线交AC于点Q；

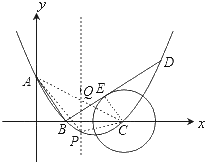
可求出AC的解析式为

设P点的坐标为

则Q点的坐标为

∴

∵

∴当m=3时，的面积最大为；

此时，P点的坐标为．

（3）相交．证明：连接CE，则，

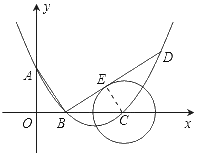
当时，

A(0,3),B(2,0),C(6,0)，

对称轴x=4，

∴ ,

∵AB⊥BD，

∴

∴△AOB∽△BEC，

∴

∵

∴抛物线的对称轴与⊙C相交．