题目内容
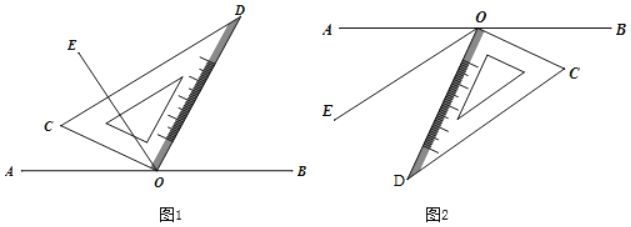
【题目】如图1直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,射线OE平分∠AOD.
(1)若∠COE=40°,则∠BOD= .
(2)若∠COE=α,求∠BOD(请用含α的代数式表示);
(3)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
【答案】(1)80°;(2)2α;(3)∠BOD+2∠COE=360°,理由见详解.
【解析】
(1)先根据直角计算∠DOE的度数,再根据角平分线的定义计算∠AOD的度数,最后利用平角的定义可得结论;
(2)先根据直角计算∠DOE的度数,再根据角平分线的定义计算∠AOD的度数,最后利用平角的定义可得结论;
(3)设∠BOD=β,则∠AOD=180°-β,根据角平分线的定义表示∠DOE,再利用角的和差关系求∠COE的度数,可得结论.
解:(1)若∠COE=40°,
∵∠COD=90°,
∴∠EOD=90°﹣40°=50°,
∵OE平分∠AOD,
∴∠AOD=2∠EOD=100°,
∴∠BOD=180°﹣100°=80°;
(2)∵∠COE=α,
∴∠EOD=90﹣α,
∵OE平分∠AOD,
∴∠AOD=2∠EOD=2(90﹣α)=180﹣2α,
∴∠BOD=180°﹣(180﹣2α)=2α;
(3)如图2,∠BOD+2∠COE=360°,理由是:
设∠BOD=β,则∠AOD=180°﹣β,
∵OE平分∠AOD,
∴∠EOD=![]() ∠AOD=
∠AOD=![]() =90°﹣
=90°﹣![]() β,
β,
∵∠COD=90°,
∴∠COE=90°+(90°﹣![]() β)=180°﹣
β)=180°﹣![]() β,
β,
即∠BOD+2∠COE=360°.
故答案为:(1)80°;(2)2α;(3)∠BOD+2∠COE=360°,理由见详解.

练习册系列答案
相关题目