题目内容
【题目】抛物线![]() 与x轴交于A、B两点,与y轴交于C,其中B(4,0),C(0,2),点P为抛物线上一动点,过点P作PQ平行BC交抛物线于Q.
与x轴交于A、B两点,与y轴交于C,其中B(4,0),C(0,2),点P为抛物线上一动点,过点P作PQ平行BC交抛物线于Q.
(1)求抛物线的解析式;
(2)①当P、Q两点重合时,PQ所在直线解析式为 ;②在①的条件下,取线段BC中点M,连接PM,判断以点P、O、M、B为顶点的四边形是什么四边形,并说明理由?
(3)已知N(0,![]() ),连接BN,K(3,0),KE∥y轴,交BN于E,x轴上有一动点F,∠EFN=60°,求OF的长.
),连接BN,K(3,0),KE∥y轴,交BN于E,x轴上有一动点F,∠EFN=60°,求OF的长.
【答案】(1)y=![]() x2-
x2-![]() x+2;(2)①y=-
x+2;(2)①y=-![]() x;②以点P、O、M、B为顶点的四边形是菱形,理由见解析;(3)
x;②以点P、O、M、B为顶点的四边形是菱形,理由见解析;(3)![]() 1或
1或![]() .
.
【解析】
(1)把B,C两点的坐标代入![]() ,得出方程组求解即可;
,得出方程组求解即可;
(2)①求出BC的解析式为y=-![]() x+2,,因PQ∥BC,可设出PQ的解析式为y=-
x+2,,因PQ∥BC,可设出PQ的解析式为y=-![]() x+n,P、Q两点重合可理解为PQ与抛物线只有一个公共点,由联立方程组得到的一元二次方程的根的判别式为0列出方程求得结果;②根据题意求出P、M点的坐标,从而得出OP、OM、BM、BP的长度便可得出结论;
x+n,P、Q两点重合可理解为PQ与抛物线只有一个公共点,由联立方程组得到的一元二次方程的根的判别式为0列出方程求得结果;②根据题意求出P、M点的坐标,从而得出OP、OM、BM、BP的长度便可得出结论;
(3)易证∠BNO=60°,在y轴上取一点L,构造等边△ENL,再作△ENL的外接圆⊙H,该圆与x轴的交点便是满足条件的F点.根据等边三角形的性质和勾股定理求得OF便可.
解:(1)把B(4,0),C(0,2)代入y=![]() x2+bx+c得,
x2+bx+c得,
![]() ,解得
,解得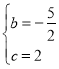 ,
,
∴抛物线的解析式为y=![]() x2-
x2-![]() x+2;
x+2;
(2)①设BC的解析式为:y=kx+m(k≠0),则
![]() ,解得
,解得 ,
,
∴直线BC的解析式为y=-![]() x+2,
x+2,
∵PQ∥BC,
∴设直线PQ的解析式为:y=-![]() x+n,
x+n,
当P、Q两点重合时,即直线PQ与抛物线只有一个公共点,
由方程组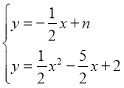 ,消去y整理得x2-4x+4-2n=0,
,消去y整理得x2-4x+4-2n=0,
∴![]() =16-16+8n=8n=0,∴n=0,
=16-16+8n=8n=0,∴n=0,
∴PQ的解析式为:y=-![]() x.
x.
故答案为:y=-![]() x;
x;
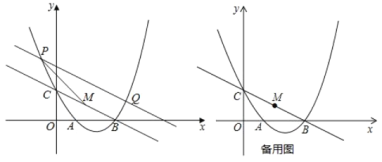
②如图1,以点P、O、M、B为顶点的四边形是菱形.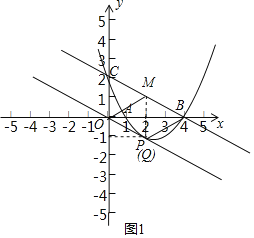
理由如下:
∵M是BC的中点,B(4,0),C(0,2),
∴M(2,1),
联立方程组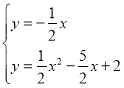 ,解得
,解得![]() ,
,
∴P(2,-1),
∴OP=PB=OM=BM=![]() ,
,
∴四边形OPBM是菱形;
(3)∵N(0,-![]() ),B(4,0),∴ON=
),B(4,0),∴ON=![]() ,OB=4,
,OB=4,
∴NB的解析式为y=![]() ,
,
∴tan∠BNO=![]() ,
,
∴∠BNO=60°,
∵K(3,0),KE∥y轴,∴∠KEB=60°,KB=1,
∴KE=![]() ,∴E(3,-
,∴E(3,-![]() ),
),
在y轴上取一点L,使得NL=NE,连接LE,则△ENL为等边三角形,过E作EG⊥y轴于G,作△ENL的外接圆⊙H,与x轴交于点F和F'点,连接FN、F'N、EF、EF'、HA,如图2,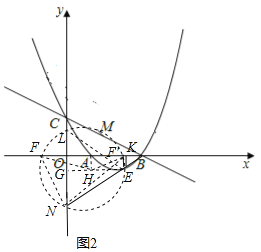
则∠EFN=∠EF'N=∠ECN=60°,点H在EG上,且HG=![]() EG=1,HA⊥x轴,HA=EK=
EG=1,HA⊥x轴,HA=EK=![]() ,HE=HF=HF'=2,
,HE=HF=HF'=2,
∴AF=AF'=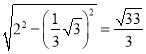 ,
,
∴OF=![]() 1,OF'=
1,OF'=![]() .
.
故OF的长为![]() 1或
1或![]() .
.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案