题目内容
 △ABC中,∠BAC=∠ACB.
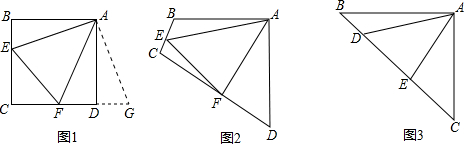
△ABC中,∠BAC=∠ACB.(1)如图,E是AB延长线上一点,连接CE,∠BEC的平分线交BC于点D,交AC于点P.
求证:∠CPD=90°-
| 1 | 2 |
(2)若E是射线BA上一点(E不与A、B重合),连接CE,∠BEC的平分线所在直线交BC于点D,交CA所在直线于点P.∠CPD与∠BCE有什么关系?请画出图形,给出你的结论,并说明理由.
分析:(1)根据角平分线的性质,等腰三角形的性质,三角形的外角性质,可得2∠CPD+∠BCE=180°,从而求解;
(2)分两种情况:i)若点E在BA上(E不与A、B重合;ii)若E在BA的延长线上;讨论求解.
(2)分两种情况:i)若点E在BA上(E不与A、B重合;ii)若E在BA的延长线上;讨论求解.
解答: (1)证明:∵EP平分∠BEC,
(1)证明:∵EP平分∠BEC,
∴∠BEP=∠CEP.
△ACE中,∠A+∠ACE+∠AEC=180°.
∵∠ACE=∠ACB+∠BCE,且∠A=∠ACB,
∴2∠A+2∠BEP+∠BCE=180°,
∴2(∠A+∠BEP)+∠BCE=180°,
∵∠CPD=∠A+∠BEP,
∴2∠CPD+∠BCE=180°,
∴∠CPD=90°-
∠BCE;
(2)结论:∠CPD=
∠BCE.理由如下:
 解:设∠CAB=∠ACB=α.
解:设∠CAB=∠ACB=α.
∵ED平分∠BEC,
∴∠BED=∠CED.
设∠BED=∠CED=β,则∠CEB=2β.
分两种情况:
i)若点E在BA上(E不与A、B重合,如图,
∵∠ACE=∠BEC-∠CAE,
∴∠ACE═2β-α.
∴∠BCE=∠ACB-∠ACE=α-(2β-α)=2α-2β.
∵∠CPD=∠CED-∠ACE,
∴∠CPD=β-(2β-α)=α-β,
∴∠CPD=
∠BCE;
ii)若E在BA的延长线上,如图,
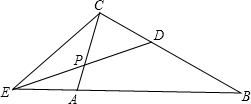 ∵∠ACE=∠CAB-∠CEB,
∵∠ACE=∠CAB-∠CEB,
∴∠ACE═α-2β,
∴∠BCE=∠ACB+∠ACE=α+(α-2β)=2α-2β.
∵∠CPD=∠ACE+∠CEP,
∴∠CPD=α-2β+β=α-β,
∴∠CPD=
∠BCE.
综上,可知∠CPD=
∠BCE.
 (1)证明:∵EP平分∠BEC,
(1)证明:∵EP平分∠BEC,∴∠BEP=∠CEP.
△ACE中,∠A+∠ACE+∠AEC=180°.
∵∠ACE=∠ACB+∠BCE,且∠A=∠ACB,
∴2∠A+2∠BEP+∠BCE=180°,
∴2(∠A+∠BEP)+∠BCE=180°,
∵∠CPD=∠A+∠BEP,
∴2∠CPD+∠BCE=180°,
∴∠CPD=90°-
| 1 |
| 2 |
(2)结论:∠CPD=
| 1 |
| 2 |
 解:设∠CAB=∠ACB=α.
解:设∠CAB=∠ACB=α.∵ED平分∠BEC,
∴∠BED=∠CED.
设∠BED=∠CED=β,则∠CEB=2β.
分两种情况:
i)若点E在BA上(E不与A、B重合,如图,
∵∠ACE=∠BEC-∠CAE,
∴∠ACE═2β-α.
∴∠BCE=∠ACB-∠ACE=α-(2β-α)=2α-2β.
∵∠CPD=∠CED-∠ACE,
∴∠CPD=β-(2β-α)=α-β,
∴∠CPD=
| 1 |
| 2 |
ii)若E在BA的延长线上,如图,
 ∵∠ACE=∠CAB-∠CEB,
∵∠ACE=∠CAB-∠CEB,∴∠ACE═α-2β,
∴∠BCE=∠ACB+∠ACE=α+(α-2β)=2α-2β.
∵∠CPD=∠ACE+∠CEP,
∴∠CPD=α-2β+β=α-β,
∴∠CPD=
| 1 |
| 2 |
综上,可知∠CPD=
| 1 |
| 2 |
点评:考查了等腰三角形的性质,三角形的外角性质,第二问注意分类思想的运用,本题有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 18、如图,在△ABC中,∠BAC=60°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是
18、如图,在△ABC中,∠BAC=60°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是 如图,△ABC中,∠BAC=60°,AB=2AC.点P在△ABC内,且PA=
如图,△ABC中,∠BAC=60°,AB=2AC.点P在△ABC内,且PA=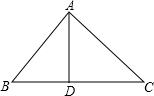 如图,在△ABC中,∠BAC=90°,AB=AC=a,AD是△ABC的高,则AD的长为
如图,在△ABC中,∠BAC=90°,AB=AC=a,AD是△ABC的高,则AD的长为 93、如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,那么△AEF是等腰三角形吗?
93、如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,那么△AEF是等腰三角形吗?