题目内容
【题目】如图1,在矩形ABCD中,AB=4,AD=5,E为射线BC上一点,DF⊥AE于F,连结DE.
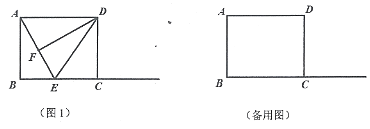
(1)当E在线段BC上时
①若DE=5,求BE的长;
②若CE=EF,求证:AD=AE;
(2)连结BF,在点E的运动过程中:
①当△ABF是以AB为底的等腰三角形时,求BE的长;
②记△ADF的面积为S1,记△DCE的面积为S2,当BF∥DE时,请直接写出S1:S2的值.
【答案】(1)①BE=2;②证明见解析;(2)①BE=2;②S1:S2=1
【解析】(1)①在矩形 ABCD 中,∠B=∠DCE=90°,BC=AD=5,DC=AB=4,由勾股定理求得CE的长,即可求得BE的长;
②证明△CED≌△DEF,可得∠CED=∠FED,从而可得∠ADE=∠AED,即可得到AD=AE;
(2)①分两种情况点 E 在线段 BC 上、点 E 在 BC 延长线上两种情况分别讨论即可得;
②S1:S2=1,当 BF//DE 时,延长 BF 交 AD 于 G,由已知可得到四边形 BEDG 是平行四边形,继而可得S△DEF=![]() S平行四边形 BEDG,S △BEF+S△ DFG=
S平行四边形 BEDG,S △BEF+S△ DFG=![]() S平行四边形 BEDG,S△ABG=S△CDE,根据面积的知差即可求得结论.
S平行四边形 BEDG,S△ABG=S△CDE,根据面积的知差即可求得结论.
(1)①在矩形 ABCD 中,∠B=∠DCE=90°,
BC=AD=5,DC=AB=4,
∵DE=5,
∴CE=![]() =3,
=3,
∴BE=BC-CE=5-3=2;
②在矩形 ABCD 中,∠DCE=90°,AD//BC,
∴∠ADE=∠DEC,∠DCE=∠DFE,
∵CE=EF,DE=DE,
∴△CED≌△DEF(HL),
∴∠CED=∠FED,
∴∠ADE=∠AED,
∴AD=AE;
(2)①当点 E 在线段 BC 上时,AF=BF,如图所示:
∴∠ABF=∠BAF,
∵∠ABF+∠EBF=90°,
∠BAF+∠BEF=90°,
∴∠EBF=∠BEF,
∴EF=BF ,∴AF=EF,
∵DF⊥AE,
∴DE=AD=5,
在矩形 ABCD 中,CD=AB=4,∠DCE=90°,
∴CE=3,
∴BE=5-3=2;

当点 E 在 BC 延长线上时,AF=BF,如图所示,
同理可证 AF=EF,

∵DF⊥AE,
∴DE=AD=5,
在矩形 ABCD 中,CD=AB=4,∠DCE=90°,
∴CE=3,
∴BE=5+3=8,
综上所述,可知BE=2或8;
②S1:S2=1,解答参考如下:
当 BF//DE 时,延长 BF 交 AD 于 G,

在矩形 ABCD 中,AD//BC,AD=BC,AB=CD,
∠BAG=∠DCE=90°,
∵BF//DE,
∴四边形 BEDG 是平行四边形,
∴BE=DG,S△DEF=![]() S平行四边形 BEDG,
S平行四边形 BEDG,
∴AG=CE,S △BEF+S△ DFG=![]() S平行四边形 BEDG,
S平行四边形 BEDG,
∴△ABG≌△CDE,
∴S△ABG=S△CDE,
∵S △ABE=![]() S平行四边形 BEDG,
S平行四边形 BEDG,
∴S△ABE=S△BEF+S△DFG,
∴S△ABF=S△DFG,
∴S△ABF+S△AFG=S△DFG+S△AFG即 S△ABG=S△ADF,
∴S△CDE=S△ADF,即 S1:S2=1.

 名师点拨卷系列答案
名师点拨卷系列答案【题目】甲、乙两校派相同人数的优秀学生,参加县教育局举办的中小学生美文诵读决赛。比赛结束后,发现学生成绩分别是7分、8分、9分或10分(满分10分),核分员依据统计数据绘制了如下尚不完整的统计图表。根据这些材料,请你回答下列问题:
甲校成绩统计表 | ||||
成绩 | 7分 | 8分 | 9分 | 10分 |
人数 | 11 | 0 | 8 | |
(1)在图①中,“7分”所在扇形的圆心角等于_______
(2)求图②中,“8分”的人数,并请你将该统计图补充完整。


(3)经计算,乙校学生成绩的平均数是8.3分,中位数是8分。请你计算甲校学生成绩的平均数、中位数,并从平均数和中位数的角度分析哪个学校的成绩较好?
(4)如果教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
【题目】某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0,每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比,经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12),符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据.
月份n(月) | 1 | 2 |
成本y(万元/件) | 11 | 12 |
需求量x(件/月) | 120 | 100 |
(1)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(2)求k,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第m个月和第(m+1)个月的利润相差最大,求m.