题目内容
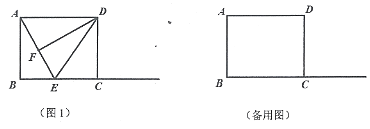
【题目】如图1,两个形状、大小完全相同的含有30゜和60゜的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
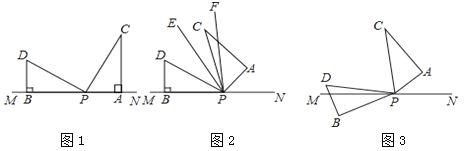
(1)试说明:∠DPC=90゜;
(2)如图2,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度,PF平分∠APD,PE平分∠CPD,求∠EPF;
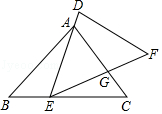
(3)如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,在两个三角板旋转过程中(PC转到与PM重合时,两三角板都停止转动),以下两个结论:①![]() 为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
为定值;②∠BPN+∠CPD为定值,请选出正确的结论,并说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)①正确,②不正确,证明见解析.
;(3)①正确,②不正确,证明见解析.
【解析】
试题分析:(1)利用含有![]() 、
、![]() 的三角板得出
的三角板得出![]() ,进而求出即可;
,进而求出即可;
(2)设![]() ,则
,则![]() ,进而利用
,进而利用![]() 求出即可;
求出即可;
(3)首先得出正确,设运动时间为![]() 秒,则
秒,则![]() ,表示出
,表示出![]() 和
和![]() 的度数即可得出答案.
的度数即可得出答案.
试题解析:(1)![]() ,
,![]()
![]() ;
;
(2)设![]() ,则
,则![]() ,
,![]()
![]()
![]()
![]()
(3)①正确.设运动时间为![]() 秒,则
秒,则![]() ,
,![]()
![]()
![]() ②
②![]() 由此可以得出
由此可以得出![]() 的值随着时间在变化,不为定值,所以②
的值随着时间在变化,不为定值,所以②

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目