题目内容
 如图,抛物线
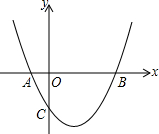
如图,抛物线 (b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(b,c是常数,且c<0)与x轴分别交于点A、B(点A位于点B的左侧),与y轴的负半轴交于点C,点A的坐标为(-1,0).
(1)请直接写出点OA的长度;
(2)若常数b,c满足关系式:bc=3.求抛物线的解析式;
(3)在(2)的条件下,点P是x轴下方抛物线上的动点,连接PB、PC.设△PBC的面积为S.
①求S的取值范围;
②若△PBC的面积S为整数,则这样的点P共有多少个(直接写出结果)?
解:∵点A的坐标为(-1,0),
∴OA=1;
(2)把点A(-1,0)代入抛物线得, -b+c=0,
-b+c=0,
∴b=c+ ,
,
∵bc=3,
∴(c+ )c=3,
)c=3,
整理得,2c2+c-6=0,
解得c1= (舍去),c2=-2,
(舍去),c2=-2,
∴b=-2+ =-
=- ,
,
抛物线解析式为y= x2-
x2- x-2;
x-2;
(3)①令y=0,则 x2-
x2- x-2=0,
x-2=0,
整理得,x2-3x-4=0,
解得x1=-1,x2=4,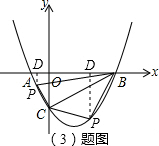
∴点B的坐标为(4,0),
∴OB=4,
设点P的横坐标为x,
点P在y轴左边时,-1<x<0,过点P作PD⊥x轴于D,
△PBC的面积S=S梯形PCOD+S△BOC-S△PBD,
= (-
(- x2+
x2+ x+2+2)•(-x)+
x+2+2)•(-x)+ ×4×2-
×4×2- (-
(- x2+
x2+ x+2)•(4-x),
x+2)•(4-x),
=x2-4x,
∵x<2时,S随x的增大而减小,
∴0<S<5;
点P在y轴右边时,0<x<4,过点P作PD⊥x轴于D,
△PBC的面积S=S梯形PCOD+S△PBD-S△BOC,
= (-
(- x2+
x2+ x+2+2)•x+
x+2+2)•x+ (-
(- x2+
x2+ x+2)•(4-x)+
x+2)•(4-x)+ ×2×4,
×2×4,
=-x2+4x,
=-(x-2)2+4,
∵a=-1<0,
∴当x=2时,S有最大值4,
∴0<S≤4;
②点P在y轴左边时,S可取的整数值为1、2、3、4,点P有4个,
点P在y轴右边时,S可取的整数值有1、2、3、4,点P有7个,
所以,使△PBC的面积S为整数的点P共有11个.
分析:(1)根据点A的坐标写出OA的长度即可;
(2)把点A的坐标代入抛物线解析式用c表示出b,然后代入bc=3计算求出c的值,再求出b的值,即可得解;
(3)①根据抛物线解析式令y=0解方程求出点B的坐标,从而得到OB的长,再分点P在y轴左边时,过点P作PD⊥x轴于D,然后根据△PBC的面积S=S梯形PCOD+S△BOC-S△PBD,列式整理,再根据二次函数的增减性求出取值范围;点P在y轴右边时,过点P作PD⊥x轴于D,然后根据△PBC的面积S=S梯形PCOD+S△PBD-S△BOC列式整理,再根据二次函数的增减性求解;
②根据S的取值范围分两部分确定出点P的个数即可得解.
点评:本题是二次函数综合题型,主要利用了二次函数图象上点的坐标特征,三角形的面积表示,二次函数的对称性以及二次函数的函数值的取值范围的求解,难点在于(3)要分情况讨论.
∴OA=1;
(2)把点A(-1,0)代入抛物线得,
 -b+c=0,
-b+c=0,∴b=c+
 ,
,∵bc=3,
∴(c+
 )c=3,
)c=3,整理得,2c2+c-6=0,
解得c1=
 (舍去),c2=-2,
(舍去),c2=-2,∴b=-2+
 =-
=- ,
,抛物线解析式为y=
 x2-
x2- x-2;
x-2;(3)①令y=0,则
 x2-
x2- x-2=0,
x-2=0,整理得,x2-3x-4=0,
解得x1=-1,x2=4,

∴点B的坐标为(4,0),
∴OB=4,
设点P的横坐标为x,
点P在y轴左边时,-1<x<0,过点P作PD⊥x轴于D,
△PBC的面积S=S梯形PCOD+S△BOC-S△PBD,
=
 (-
(- x2+
x2+ x+2+2)•(-x)+
x+2+2)•(-x)+ ×4×2-
×4×2- (-
(- x2+
x2+ x+2)•(4-x),
x+2)•(4-x),=x2-4x,
∵x<2时,S随x的增大而减小,
∴0<S<5;
点P在y轴右边时,0<x<4,过点P作PD⊥x轴于D,
△PBC的面积S=S梯形PCOD+S△PBD-S△BOC,
=
 (-
(- x2+
x2+ x+2+2)•x+
x+2+2)•x+ (-
(- x2+
x2+ x+2)•(4-x)+
x+2)•(4-x)+ ×2×4,
×2×4,=-x2+4x,
=-(x-2)2+4,
∵a=-1<0,
∴当x=2时,S有最大值4,
∴0<S≤4;
②点P在y轴左边时,S可取的整数值为1、2、3、4,点P有4个,
点P在y轴右边时,S可取的整数值有1、2、3、4,点P有7个,
所以,使△PBC的面积S为整数的点P共有11个.
分析:(1)根据点A的坐标写出OA的长度即可;
(2)把点A的坐标代入抛物线解析式用c表示出b,然后代入bc=3计算求出c的值,再求出b的值,即可得解;
(3)①根据抛物线解析式令y=0解方程求出点B的坐标,从而得到OB的长,再分点P在y轴左边时,过点P作PD⊥x轴于D,然后根据△PBC的面积S=S梯形PCOD+S△BOC-S△PBD,列式整理,再根据二次函数的增减性求出取值范围;点P在y轴右边时,过点P作PD⊥x轴于D,然后根据△PBC的面积S=S梯形PCOD+S△PBD-S△BOC列式整理,再根据二次函数的增减性求解;
②根据S的取值范围分两部分确定出点P的个数即可得解.
点评:本题是二次函数综合题型,主要利用了二次函数图象上点的坐标特征,三角形的面积表示,二次函数的对称性以及二次函数的函数值的取值范围的求解,难点在于(3)要分情况讨论.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG| 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4). 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由. .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.