题目内容
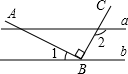（2012•鄂尔多斯）如图，直线a∥b，点B在直线b上，且AB⊥BC，∠1=35°24′，则∠2的度数为125°24′
125°24′
．分析：由直线a∥b，根据两直线平行，内错角相等，即可求得∠BAC的度数，又由AB⊥BC，根据三角形外角的性质，即可求得∠2的度数．
解答：解：∵直线a∥b，∠1=35°24′，
∴∠BAC=∠1=35°24′，
∵AB⊥BC，
∴∠ABC=90°，
∴∠2=∠BAC+∠ABC=35°24′+90°=125°24′．
故答案为：125°24′．
∴∠BAC=∠1=35°24′，
∵AB⊥BC，
∴∠ABC=90°，
∴∠2=∠BAC+∠ABC=35°24′+90°=125°24′．
故答案为：125°24′．
点评：此题考查了平行线的性质以及三角形外角的性质．此题比较简单，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
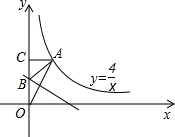（2012•鄂尔多斯）如图，点A在双曲线
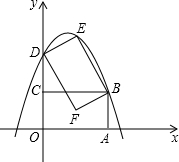，点O的对应点为点D，点C的对应点为点E，且点D恰好在y轴上，二次函数y=ax2+bx+2的图象过E、B两点．
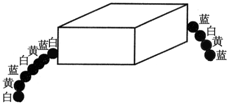（2012•鄂尔多斯）有一串彩色的珠子，按白黄蓝的顺序重复排列，其中有一部分放在盒子里，如图所示，则这串珠子被放在盒子里的颗数可能是（ ）
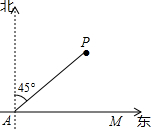（2012•鄂尔多斯）如图，海中有一小岛P，在距小岛
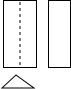（2012•鄂尔多斯）一个几何体的三视图如图所示，那么这个几何体是（ ）