题目内容
(2012•鄂尔多斯)如图所示,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,且OA=
,OC=1.矩形OABC绕点B按顺时针方向旋转60°后得到矩形DFBE.点A的对应点为点F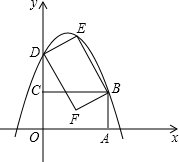 ,点O的对应点为点D,点C的对应点为点E,且点D恰好在y轴上,二次函数y=ax2+bx+2的图象过E、B两点.
,点O的对应点为点D,点C的对应点为点E,且点D恰好在y轴上,二次函数y=ax2+bx+2的图象过E、B两点.
(1)请直接写出点B和点D的坐标;
(2)求二次函数的解析式;
(3)在x轴上方是否存在点P,点Q,使以点O、A、P、Q为顶点的平行四边形的面积是矩形OABC面积的2倍,且点P在抛物线上?若存在,求出点P,点Q的坐标;若不存在,请说明理由.
| 3 |
 ,点O的对应点为点D,点C的对应点为点E,且点D恰好在y轴上,二次函数y=ax2+bx+2的图象过E、B两点.
,点O的对应点为点D,点C的对应点为点E,且点D恰好在y轴上,二次函数y=ax2+bx+2的图象过E、B两点.(1)请直接写出点B和点D的坐标;
(2)求二次函数的解析式;
(3)在x轴上方是否存在点P,点Q,使以点O、A、P、Q为顶点的平行四边形的面积是矩形OABC面积的2倍,且点P在抛物线上?若存在,求出点P,点Q的坐标;若不存在,请说明理由.
分析:(1)根据OA=
,OC=1,可得出点B的坐标,根据函数解析式可得出点D的坐标;
(2)过点E作EM⊥于BC点M,根据旋转角度可得出∠EBM=60°,结合BE=
,可得出点E的坐标,将点E和点B的坐标代入可得出二次函数解析式;
(3)设点P的坐标为(x,-
x2+
x+2),然后根据平行四边形OAPQ的面积是矩形OABC面积的2倍,可得出x的值,继而可求出点P的坐标及点Q的坐标.
| 3 |
(2)过点E作EM⊥于BC点M,根据旋转角度可得出∠EBM=60°,结合BE=
| 3 |
(3)设点P的坐标为(x,-
| 4 |
| 3 |
| 3 |
解答:解:(1)∵OA=
,OC=1,
∴点B的坐标为(
,1),
根据二次函数解析式为y=ax2+bx+2,可得点D的坐标为(0,2);
综上可得点B的坐标为(
,1),点D的坐标为(0,2).
(2)过点E作EM⊥于BC点M,

∵∠EBM=60°,BE=
,
∴BM=
,EM=
,
∴CM=BC-BM=
-
=
,
∴点E的坐标为(
,
),
将点E及点B的坐标代入可得:
,
解得:
,
故函数解析式为y=-
x2+
x+2;
(3)存在.
设点P的坐标为(x,-
x2+
x+2),
∵平行四边形OAPQ的面积是矩形OABC面积的2倍,
∴
×(-
x2+
x+2)=2
,
解得:x1=
,x2=0,
当x=0时,点P的坐标为(0,2),此时点Q的坐标为(
,2)或(-
,2);
当x=
时,点P的坐标为(
,2),此时点Q的坐标为(
,2)或(-
,2);
| 3 |
∴点B的坐标为(
| 3 |
根据二次函数解析式为y=ax2+bx+2,可得点D的坐标为(0,2);
综上可得点B的坐标为(
| 3 |
(2)过点E作EM⊥于BC点M,

∵∠EBM=60°,BE=
| 3 |
∴BM=
| ||
| 2 |
| 3 |
| 2 |
∴CM=BC-BM=
| 3 |
| ||
| 2 |
| ||
| 2 |
∴点E的坐标为(
| ||
| 2 |
| 5 |
| 2 |
将点E及点B的坐标代入可得:
|
解得:
|
故函数解析式为y=-
| 4 |
| 3 |
| 3 |
(3)存在.
设点P的坐标为(x,-
| 4 |
| 3 |
| 3 |
∵平行四边形OAPQ的面积是矩形OABC面积的2倍,
∴
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
解得:x1=
| 3 |
| 4 |
| 3 |
当x=0时,点P的坐标为(0,2),此时点Q的坐标为(
| 3 |
| 3 |
当x=
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 7 |
| 4 |
| 3 |
| ||
| 4 |
点评:本题考查了二次函数综合题,涉及了待定系数法求函数解析式、旋转角度、解直角三角形及平行四边形的性质,综合性较强,解答本题的关键是熟练掌握各个知识点的内容,仔细理解题意,将所学的知识融会贯通,难度较大.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 (2012•鄂尔多斯)如图,点A在双曲线
(2012•鄂尔多斯)如图,点A在双曲线 (2012•鄂尔多斯)有一串彩色的珠子,按白黄蓝的顺序重复排列,其中有一部分放在盒子里,如图所示,则这串珠子被放在盒子里的颗数可能是( )
(2012•鄂尔多斯)有一串彩色的珠子,按白黄蓝的顺序重复排列,其中有一部分放在盒子里,如图所示,则这串珠子被放在盒子里的颗数可能是( ) (2012•鄂尔多斯)如图,海中有一小岛P,在距小岛
(2012•鄂尔多斯)如图,海中有一小岛P,在距小岛 (2012•鄂尔多斯)一个几何体的三视图如图所示,那么这个几何体是( )
(2012•鄂尔多斯)一个几何体的三视图如图所示,那么这个几何体是( )