题目内容
 (2012•鄂尔多斯)如图,海中有一小岛P,在距小岛24
(2012•鄂尔多斯)如图,海中有一小岛P,在距小岛24| 3 |
分析:过P作PC⊥AM于C,则PC的长是A沿AM方向距离P点的最短距离,求出PC长和24
比较即可.
| 3 |
解答:解: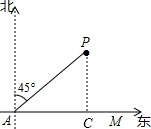
过P作PC⊥AM于C,
则∠PCA=90°且PC的长是A沿AM方向距离P点的最短距离,
∵∠PAM=90°-45°=45°,
∴∠APC=45°=∠PAC,
∴PC=AC,
由勾股定理得:2PC2=AP2=482,
∴PC=24
海里<24
海里,
∴轮船继续向正东方向航行,有触礁的危险;
设A沿AD方向运动,正好没有触礁的危险,如图:
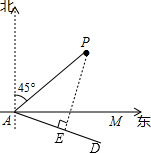
过P作PE⊥AD,于E,则此时PE=24
海里,
在Rt△PAE中,由勾股定理得:AE=
=24,
即AE=
AP,
∴∠APE=30°,
∴∠PAE=60°,
∠MAD=60°-45°=15°,
即轮船自A处开始至少沿东偏南15度方向航行,才能安全通过这一海域.

过P作PC⊥AM于C,
则∠PCA=90°且PC的长是A沿AM方向距离P点的最短距离,
∵∠PAM=90°-45°=45°,
∴∠APC=45°=∠PAC,
∴PC=AC,
由勾股定理得:2PC2=AP2=482,
∴PC=24
| 2 |
| 3 |
∴轮船继续向正东方向航行,有触礁的危险;
设A沿AD方向运动,正好没有触礁的危险,如图:

过P作PE⊥AD,于E,则此时PE=24
| 3 |
在Rt△PAE中,由勾股定理得:AE=
482-(24
|
即AE=
| 1 |
| 2 |
∴∠APE=30°,
∴∠PAE=60°,
∠MAD=60°-45°=15°,
即轮船自A处开始至少沿东偏南15度方向航行,才能安全通过这一海域.
点评:本题考查了解直角三角形的应用,关键是如何构造直角三角形并知道求哪一条线段的长,题目比较典型,是一道比较好的题目.

练习册系列答案
相关题目
 (2012•鄂尔多斯)如图,点A在双曲线
(2012•鄂尔多斯)如图,点A在双曲线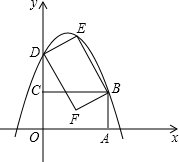 ,点O的对应点为点D,点C的对应点为点E,且点D恰好在y轴上,二次函数y=ax2+bx+2的图象过E、B两点.
,点O的对应点为点D,点C的对应点为点E,且点D恰好在y轴上,二次函数y=ax2+bx+2的图象过E、B两点. (2012•鄂尔多斯)有一串彩色的珠子,按白黄蓝的顺序重复排列,其中有一部分放在盒子里,如图所示,则这串珠子被放在盒子里的颗数可能是( )
(2012•鄂尔多斯)有一串彩色的珠子,按白黄蓝的顺序重复排列,其中有一部分放在盒子里,如图所示,则这串珠子被放在盒子里的颗数可能是( ) (2012•鄂尔多斯)一个几何体的三视图如图所示,那么这个几何体是( )
(2012•鄂尔多斯)一个几何体的三视图如图所示,那么这个几何体是( )