题目内容
 (2012•鄂尔多斯)如图,点A在双曲线y=
(2012•鄂尔多斯)如图,点A在双曲线y=| 4 |
| x |
2
| 6 |
2
.| 6 |
分析:由OA的垂直平分线交OC于点B可知OB=AB,故△ABC的周长=AC+OC,设A(a,b),由于点A在第一象限,故a>0,b>0,根据AC⊥y轴可知AC2+OC2=OA2,再根据点A在反比例函数y=
的图象上可知b=
,由此可组成关于a、b的方程组,求出a+b的值即可.
| 4 |
| x |
| 4 |
| a |
解答:解:∵OA的垂直平分线交OC于点B,
∴OB=AB,
∴△ABC的周长=AC+OC,
设A(a,b),
∵点A在第一象限,
∴a>0,b>0,
∴AC+OC=a+b,
∵AC⊥y轴,OA=4,
∴AC2+OC2=OA2,即a2+b2=16①,
∵点A在反比例函数y=
的图象上,
∴b=
②,
由①②得,a+b=2
,即△ABC的周长为2
.
故答案为:2
.
∴OB=AB,
∴△ABC的周长=AC+OC,
设A(a,b),
∵点A在第一象限,
∴a>0,b>0,
∴AC+OC=a+b,
∵AC⊥y轴,OA=4,
∴AC2+OC2=OA2,即a2+b2=16①,
∵点A在反比例函数y=
| 4 |
| x |
∴b=
| 4 |
| a |
由①②得,a+b=2
| 6 |
| 6 |
故答案为:2
| 6 |
点评:本题考查的是反比例函数综合题,此题涉及到线段垂直平分线的性质、勾股定理及反比例函数图象上点的坐标特点,在解答此题时要注意利用数形结合.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
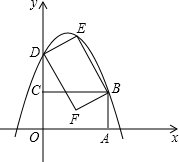 ,点O的对应点为点D,点C的对应点为点E,且点D恰好在y轴上,二次函数y=ax2+bx+2的图象过E、B两点.
,点O的对应点为点D,点C的对应点为点E,且点D恰好在y轴上,二次函数y=ax2+bx+2的图象过E、B两点. (2012•鄂尔多斯)有一串彩色的珠子,按白黄蓝的顺序重复排列,其中有一部分放在盒子里,如图所示,则这串珠子被放在盒子里的颗数可能是( )
(2012•鄂尔多斯)有一串彩色的珠子,按白黄蓝的顺序重复排列,其中有一部分放在盒子里,如图所示,则这串珠子被放在盒子里的颗数可能是( ) (2012•鄂尔多斯)如图,海中有一小岛P,在距小岛
(2012•鄂尔多斯)如图,海中有一小岛P,在距小岛 (2012•鄂尔多斯)一个几何体的三视图如图所示,那么这个几何体是( )
(2012•鄂尔多斯)一个几何体的三视图如图所示,那么这个几何体是( )