Question

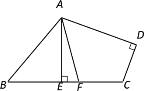
【题目】如图,△ABC中，∠ACB=90°，点F在AC延长线上，，DE是△ABC中位线，如果∠1=30°，DE=2，则四边形AFED的周长是________

Answer 1

【答案】16.

【解析】

试题根据三角形的中位线平行于第三边并且等于第三边的一半可得DE=AC，从而得到CF=DE，再根据直角三角形30°角所对的直角边等于斜边的一半可得EF=2CF，利用勾股定理列式求出CE，再求出BC，然后利用勾股定理列式求出AB，从而得到AD的长度，最后根据四边形的周长的定义列式计算即可得解：

∵DE是△ABC中位线，∴DE=AC.

∵CF=AC，∴CF=DE=2.

∵∠1=30°，∠ACB=90°，∴EF=2CF=2×2=4.

由勾股定理得，.

∴BC=2CE=.

又∵AC=2DE=2×2=4，

∴.

∴AD=AB=4，

∴四边形AFED的周长=4+（4+2）+4+2=16．