题目内容
如图,AB是⊙O的直径, ,AB=5,BD=4,则sin∠ECB= .
,AB=5,BD=4,则sin∠ECB= .
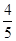 .
.
解析试题解析:连接AD,在Rt△ABD中利用勾股定理求出AD,证明△DAC∽△DBA,利用对应边成比例的知识,可求出CD、AC,继而根据sin∠ECB=sin∠DCA=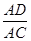 ,即可得出答案.
,即可得出答案.
连接AD,则∠ADB=90°,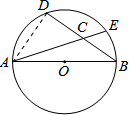
在Rt△ABD中,AB=5,BD=4,
则AD=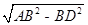 =3,
=3,
∵ ,
,
∴∠DAC=∠DBA,
∴△DAC∽△DBA,
∴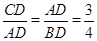 ,
,
∴CD=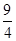 ,
,
∴AC=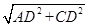 =
=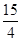 ,
,
∴sin∠ECB=sin∠DCA=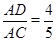 .
.
故答案为: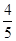 .
.
考点: (1)相似三角形的判定与性质;(2)圆周角定理;(3)锐角三角函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则
,则 .
. ;②点F是GE的中点;③AF=
;②点F是GE的中点;③AF=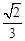 AB;④S△ABC ="5" S△BDF,其中正确的结论序号是_____________.
AB;④S△ABC ="5" S△BDF,其中正确的结论序号是_____________.
 DC.则图中阴影部分面积为 .
DC.则图中阴影部分面积为 .

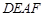 内接于△
内接于△ ,已知
,已知 ,
,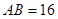 ,那么正方形的边长是 .
,那么正方形的边长是 .
 AC,AB=10时,求线段BO的长度.
AC,AB=10时,求线段BO的长度.