题目内容
如图,OABC是一个放在平面直角坐标系中的矩形,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=3,OC=4,平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线运动的时间为t(秒).
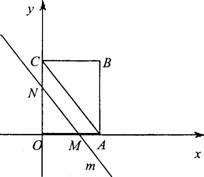
(1)写出点B的坐标;
(2)t为何值时,MN=![]() AC;
AC;
(3)设△OMN的面积为S,求S与t的函数关系式,并写出t的取值范围;当t为何值时,S有最大值?并求S的最大值.
(1)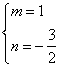
(2)直线PC的解析式是y=![]() x-
x-![]()
(3) 以点A为圆心、直径为5的圆与直线PC相离.
【解析】
试题分析:解:(1)由已知条件可知:抛物线y=![]() x2+mx+n经过A(-3,0)、B(1,0)两点.
x2+mx+n经过A(-3,0)、B(1,0)两点.
∴ 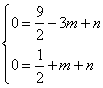 解得
解得 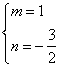
∴y=![]() x2+x-
x2+x-![]() .
.
(2)∵y=![]() x2+x-
x2+x-![]()
∴P(-1,-2),C-![]() .
.
设直线PC的解析式是y=kx+b,则 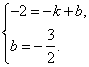 解得
解得 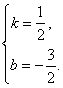
∴直线PC的解析式是y=![]() x-
x-![]() .
.
(3)如图,过点A作AE⊥PC,垂足为E.
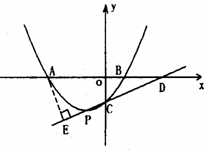
设直线PC与x轴交于点D,则点D的坐标为(3,0)
在Rt△OCD中,∵OC=![]() ,OD=3,
,OD=3,
∵CD=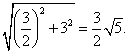
∵OA=3,OD=3,∴AD=6.
∵∠COD=∠AED=90°,∠CDO为公共角,
∴△COD~△AED.
∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∴AE=![]() .
.
∵![]() ≈2.688>2.5,
≈2.688>2.5,
∴以点A为圆心、直径为5的圆与直线PC相离.
考点:抛物线
点评:本题难度中等,主要考查学生对二次函数及抛物线图像知识点的掌握。为中考常考题型,要求学生牢固掌握,注意数形结合应用。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 别交于点M、N,直线运动的时间为t(秒).
别交于点M、N,直线运动的时间为t(秒).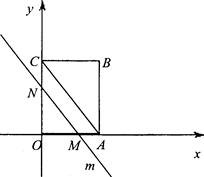
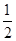 AC;
AC; AC;
AC;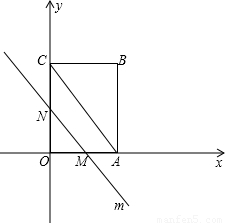
 AC;
AC;