题目内容
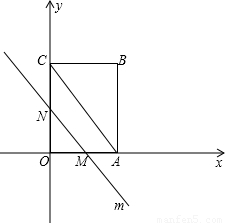
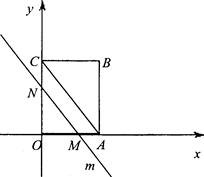
如图,OABC是一个放在平面直角坐标系中的矩形,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=3,OC=4,平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线运动的时间为t(秒).(1)写出点B的坐标;
(2)t为何值时,MN=
 AC;
AC;(3)设△OMN的面积为S,求S与t的函数关系式,并写出t的取值范围;当t为何值时,S有最大值?并求S的最大值.

【答案】分析:(1)由于四边形OABC是矩形,可直接根据OA、OC的长写出B点的坐标;
(2)此题要分两种情况考虑:
①M在线段OA上,N在线段OC上时,即0<t≤3时,若MN= AC,则MN是△OAC的中位线,此时OA=2OM,据此可求出t的值;
AC,则MN是△OAC的中位线,此时OA=2OM,据此可求出t的值;
②M在线段AB上,N在线段BC上时,即3<t<6时,若MN= AC,则MN是△ABC的中位线,设直线m与x轴的交点为D,可证得△AMD≌△BMN,由此可得BN=AD,进而可求出OD的长及t的值;
AC,则MN是△ABC的中位线,设直线m与x轴的交点为D,可证得△AMD≌△BMN,由此可得BN=AD,进而可求出OD的长及t的值;
(3)参照(2)的解题思路,此题也要分作两种情况:
①当0<t≤3时,M在线段OA上,N在线段OC上;可用t分别表示出OM、ON的长,进而可求出S、t的函数关系式;
②当3<t<6时,M在线段AB上,N在线段BC上;此时△OMN的面积,可由矩形OABC、△OMD、△OCN的面积差求得;
得出相关的函数解析式后,根据函数的性质及对应的自变量的取值范围,即可求出S的最大值及对应的t的值.
解答:解:(1)点B的坐标是(3,4);(1分)
(2)当0<t≤3时,∵MN∥AC,且MN= AC,
AC,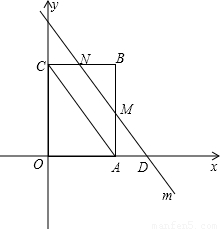
∴M是AB的中点;
∴t=1.5秒;
当3<t<6时,
设直线m与x轴交点为D,
∵MN∥AC且MN= AC,
AC,
∴M为AB的中点;
可证:△AMD≌△BMN;
∴BN=AD=t-3;
∴△BMN∽△BAC;
∴
∴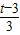 =
= ;
;
∴t=4.5秒;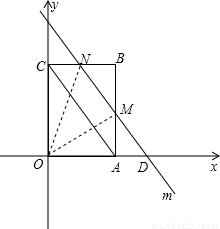
当t=1.5秒或t=4.5秒时,MN= AC;(3分)
AC;(3分)
(3)当0<t≤3时,OM=t;
由△OMN∽△OAC,得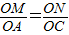 ,
,
∴ON= t,S=
t,S= t2;(4分)
t2;(4分)
当3<t<6时,
∵OD=t,
∴AD=t-3;
易知四边形ADNC是平行四边形,
∴CN=AD=t-3,BN=6-t;
由△BMN∽△BAC,可得BM= BN=8-
BN=8- t,
t,
∴AM=-4+ t;
t;
S=S矩形OABC-SRt△OAM-SRt△MBN-SRt△NCO
=12- (-4+
(-4+ t)-
t)- ×(8-
×(8- t)(6-t)-
t)(6-t)- (t-3)
(t-3)
=- t2+4t;
t2+4t;
当0<t≤3时,
∵抛物线S= t2的开口向上,在对称轴t=0的右边,S随t的增大而增大,
t2的开口向上,在对称轴t=0的右边,S随t的增大而增大,
∴当t=3时,S可取到最大值 ×32=6.
×32=6.
当3<t<6时,
∵抛物线S=- t2+4t的开口向下,它的顶点是(3,6),
t2+4t的开口向下,它的顶点是(3,6),
∴S<6;(8分)
综上,当t=3时,S有最大值6.
点评:本题是二次函数的综合题型,其中涉及到的知识点有矩形的性质、三角形中位线定理、全等三角形及相似三角形的判定和性质、二次函数的应用等.在求有关动点问题时要注意分析题意分情况讨论结果.
(2)此题要分两种情况考虑:
①M在线段OA上,N在线段OC上时,即0<t≤3时,若MN=
 AC,则MN是△OAC的中位线,此时OA=2OM,据此可求出t的值;
AC,则MN是△OAC的中位线,此时OA=2OM,据此可求出t的值;②M在线段AB上,N在线段BC上时,即3<t<6时,若MN=
 AC,则MN是△ABC的中位线,设直线m与x轴的交点为D,可证得△AMD≌△BMN,由此可得BN=AD,进而可求出OD的长及t的值;
AC,则MN是△ABC的中位线,设直线m与x轴的交点为D,可证得△AMD≌△BMN,由此可得BN=AD,进而可求出OD的长及t的值;(3)参照(2)的解题思路,此题也要分作两种情况:
①当0<t≤3时,M在线段OA上,N在线段OC上;可用t分别表示出OM、ON的长,进而可求出S、t的函数关系式;
②当3<t<6时,M在线段AB上,N在线段BC上;此时△OMN的面积,可由矩形OABC、△OMD、△OCN的面积差求得;
得出相关的函数解析式后,根据函数的性质及对应的自变量的取值范围,即可求出S的最大值及对应的t的值.
解答:解:(1)点B的坐标是(3,4);(1分)
(2)当0<t≤3时,∵MN∥AC,且MN=
 AC,
AC,
∴M是AB的中点;
∴t=1.5秒;
当3<t<6时,
设直线m与x轴交点为D,
∵MN∥AC且MN=
 AC,
AC,∴M为AB的中点;
可证:△AMD≌△BMN;
∴BN=AD=t-3;
∴△BMN∽△BAC;
∴

∴
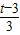 =
= ;
;∴t=4.5秒;

当t=1.5秒或t=4.5秒时,MN=
 AC;(3分)
AC;(3分)(3)当0<t≤3时,OM=t;
由△OMN∽△OAC,得
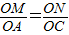 ,
,∴ON=
 t,S=
t,S= t2;(4分)
t2;(4分)当3<t<6时,
∵OD=t,
∴AD=t-3;
易知四边形ADNC是平行四边形,
∴CN=AD=t-3,BN=6-t;
由△BMN∽△BAC,可得BM=
 BN=8-
BN=8- t,
t,∴AM=-4+
 t;
t;S=S矩形OABC-SRt△OAM-SRt△MBN-SRt△NCO
=12-
 (-4+
(-4+ t)-
t)- ×(8-
×(8- t)(6-t)-
t)(6-t)- (t-3)
(t-3)=-
 t2+4t;
t2+4t;当0<t≤3时,
∵抛物线S=
 t2的开口向上,在对称轴t=0的右边,S随t的增大而增大,
t2的开口向上,在对称轴t=0的右边,S随t的增大而增大,∴当t=3时,S可取到最大值
 ×32=6.
×32=6.当3<t<6时,
∵抛物线S=-
 t2+4t的开口向下,它的顶点是(3,6),
t2+4t的开口向下,它的顶点是(3,6),∴S<6;(8分)
综上,当t=3时,S有最大值6.
点评:本题是二次函数的综合题型,其中涉及到的知识点有矩形的性质、三角形中位线定理、全等三角形及相似三角形的判定和性质、二次函数的应用等.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
相关题目
 别交于点M、N,直线运动的时间为t(秒).
别交于点M、N,直线运动的时间为t(秒).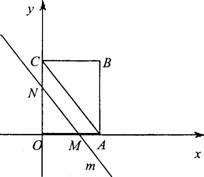
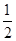 AC;
AC; AC;
AC;