��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�������AOCB�ı߳�Ϊ1����D��x����������ϣ�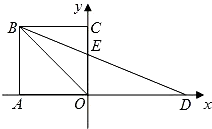 ��OD=OB��BD��OC�ڵ�E��
��OD=OB��BD��OC�ڵ�E����1�����BEC�Ķ�����
��2�����E�����ꣻ
��3�����B��O��D����������ߵĽ���ʽ����������Ҫ���ĸ���������ο����ϣ��ѷ�ĸ�еĸ��Ż�ȥ���з�ĸ�����������磺
��
| 2 | ||
|
2
| ||||
|
2
| ||
| 5 |
��
| 1 | ||
|
1��(
| ||||
(
|
| 2 |
��
| 1 | ||||
|
| ||||||||
(
|
| ||||
| 2 |
��������1����ͼ��֪��CBE=��OBD=
��OBC������⣮
��2���������������ε��������OE��ֵ��Ȼ������E�����꣮
��3�����B��O��D����������ߵĽ���ʽΪy=ax2+bx+c�����������ɵý���ʽ��
| 1 |
| 2 |
��2���������������ε��������OE��ֵ��Ȼ������E�����꣮
��3�����B��O��D����������ߵĽ���ʽΪy=ax2+bx+c�����������ɵý���ʽ��
����⣺��1�����CBE=��OBD=
��OBC=
��45��=22.5�㣬
���BEC=90��-��CBE=90��-22.5��=67.5�㣻
��2����BC��OD��
��
=
��
��
=
��
��ã�EO=2-
��
���E�������ǣ�0��2-
����
��3�����B��O��D����������ߵĽ���ʽΪy=ax2+bx+c��
��B��-1��1����O��0��0����D��
��0����
��
��
��ã�a=-1+
��b=-2+
��c=0��
��������������ߵĽ���ʽΪy=��-1+
��x2+��-2+
��x��
| 1 |
| 2 |
| 1 |
| 2 |
���BEC=90��-��CBE=90��-22.5��=67.5�㣻
��2����BC��OD��
��
| BC |
| DO |
| EC |
| EO |
��
| 1 | ||
|
| 1-EO |
| EO |
��ã�EO=2-
| 2 |
���E�������ǣ�0��2-
| 2 |
��3�����B��O��D����������ߵĽ���ʽΪy=ax2+bx+c��
��B��-1��1����O��0��0����D��
| 2 |
��
|
��ã�a=-1+
| 2 |
| 2 |
��������������ߵĽ���ʽΪy=��-1+
| 2 |
| 2 |
���������⿼����Ƕ��κ������ۺ��⣬���ô���ϵ�����������ʽ���Ѷ��еȣ�

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD�� ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ����� ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ��������� ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��