Question

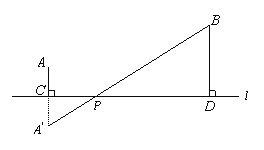
【题目】如图，小区A与公路l的距离AC＝200米，小区B与公路l的距离BD＝400米，已知CD＝800米，现要在公路旁建造一利民超市P，使P到A、B两小区的路程之和最短，超市应建在哪？

（1）请在图中画出点P；

（2）求CP的长度；

（3）求PA＋PB的最小值.

Answer 1

【答案】（1）画图见解析；（2）；（3）1000.

【解析】

试题分析：（1）利用轴对称转化为两点之间线段最短，可找到点P；（2）利用平面直角坐标系，转化为一次函数与x轴交点坐标可求得CP长度；（3）利用勾股定理求最小值.

试题解析：

（1）所以，点P为所求做点.

（2）建立如图的平面直角坐标系：则A′（0，－200），B′（800，400），设A′B：y＝kx＋b，把A（0，－200），B（800，400）分别代入， 得k ＝， b＝－200，∴A′B：y＝x－200，当y＝0时，x＝．∴CP为米．

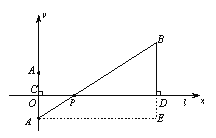
（3）由对称性得PA＋PB的最小值为线段A′B的长，作A′E⊥BE于点E，在Rt△A′BE中，

求得A′B＝1000，∴PA＋PB的最小值＝1000米.