题目内容
【题目】如图,已知⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°
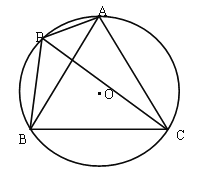
(1)当点P位于![]() 的什么位置时,四边形APBC的面积最大?并求出最大面积;
的什么位置时,四边形APBC的面积最大?并求出最大面积;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论.
【答案】(1)点P为![]() 的中点;
的中点;![]() .(2)CP=BP+AP.
.(2)CP=BP+AP.
【解析】
试题(1)过点P作PE⊥AB,垂足为E,过点C作CF⊥AB,垂足为F,把四边形的面积转化为两个三角形的面积进行计算,当点P为![]() 的中点时,PE+CF=PC从而得出最大面积.
的中点时,PE+CF=PC从而得出最大面积.
(2)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得.
试题解析:(1)当点P为![]() 的中点时,四边形APBC的面积最大.
的中点时,四边形APBC的面积最大.
理由如下,如图1,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵![]()
∴S四边形APBC=![]() AB(PE+CF),
AB(PE+CF),
当点P为![]() 的中点时,PE+CF=PC,PC为⊙O的直径,
的中点时,PE+CF=PC,PC为⊙O的直径,
∴此时四边形APBC的面积最大.
又∵⊙O的半径为1,
∴其内接正三角形的边长AB=![]() ,
,
∴S四边形APBC=![]() ×2×
×2×![]() =
=![]() .
.
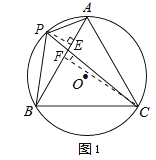
(2)在PC上截取PD=AP,如图2,
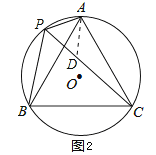
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
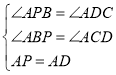 ,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.

【题目】为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
人数(人) | 4 | 8 | 8 | 10 | x | 2 |
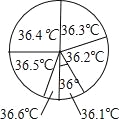
A.这些体温的众数是8
B.这些体温的中位数是36.35
C.这个班有40名学生
D.x=8