题目内容
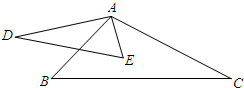（2011•西双版纳）如图，∠DAB=∠CAE，添加一个条件：∠D=∠B或∠AED=∠C或AD：AB=AE：AC或AD•AC=AB•AE（任意一个即可）
∠D=∠B或∠AED=∠C或AD：AB=AE：AC或AD•AC=AB•AE（任意一个即可）
使得△ADE∽△ACB．分析：根据相似三角形的判定方法，已知一组角相等则再添加一组相等的角或该角的两个边对应成比例即可推出两三角形相似．
解答：解：根据相似三角形的判定：两角对应相等，两三角形相似；两边对应成比例且夹角相等，两三角形相似．
已知∠DAB=∠CAE，则∠DAE=∠BAC，要使△ABC∽△ADE，则补充的一个条件可以是∠B=∠D或∠AED=∠ACB、AD：AB=AB：AC．
故答案为：∠D=∠B或∠AED=∠C或AD：AB=AE：AC或AD•AC=AB•AE（任意一个即可）．
已知∠DAB=∠CAE，则∠DAE=∠BAC，要使△ABC∽△ADE，则补充的一个条件可以是∠B=∠D或∠AED=∠ACB、AD：AB=AB：AC．
故答案为：∠D=∠B或∠AED=∠C或AD：AB=AE：AC或AD•AC=AB•AE（任意一个即可）．
点评：此题考查了相似三角形的判定．相似三角形的判定方法：①如果两个三角形的三组对应边的比相等，那么这两个三角形相似；②如果两个三角形的两条对应边的比相等，且夹角相等，那么这两个三角形相似；③如果两个三角形的两个对应角相等，那么这两个三角形相似．平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似．
练习册系列答案
相关题目
（2011•西双版纳）如图，E、F是四边形ABCD的对角线BD上的两点，BF=DE，AE=CF，∠1=∠2．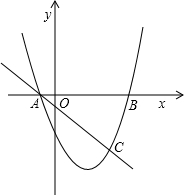
（2011•西双版纳）如图，抛物线与x轴交于A、B两点，直线y=kx-1与抛物线交于A、C两点，其中A（-1，0），B（3，0），点C的纵坐标为-3．