题目内容
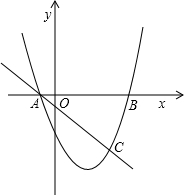 (2011•西双版纳)如图,抛物线与x轴交于A、B两点,直线y=kx-1与抛物线交于A、C两点,其中A(-1,0),B(3,0),点C的纵坐标为-3.
(2011•西双版纳)如图,抛物线与x轴交于A、B两点,直线y=kx-1与抛物线交于A、C两点,其中A(-1,0),B(3,0),点C的纵坐标为-3.(1)求k的值;
(2)求抛物线的解析式;
(3)抛物线上是否存在点P,使得△ACP是以AC为底边的等腰三角形?如果存在,写出所有满足条件的点P的坐标;如果不存在,请说明理由.
分析:(1)把(-1,0)代入y=kx-1,即可求得k的值;
(2)首先求得C的坐标,然后利用待定系数法即可求得函数的解析式;
(3)P在AC的中垂线上,首先求得AC的中垂线的解析式,然后与二次函数的解析式组成方程组,即可求得P的坐标.
(2)首先求得C的坐标,然后利用待定系数法即可求得函数的解析式;
(3)P在AC的中垂线上,首先求得AC的中垂线的解析式,然后与二次函数的解析式组成方程组,即可求得P的坐标.
解答:解:(1)把(-1,0)代入y=kx-1,得:-k-1=0,解得:k=-1;
(2)在y=-x-1中,令y=-3,解得:-x-1=-3,解得:x=2,则C的坐标是(2,-3).
设抛物线的解析式是:y=ax2+bx+c,
则
,
解得:
,
则函数的解析式是:y=x2-2x-3;
(3)A、C的中点是:(
,-
),
∵△ACP是等腰三角形,且以AC为底边,
∴P在AC的中垂线上,
∴设AC的中垂线的解析式是:y=x+c,把(
,-
)代入得:
+c=-
,解得:c=-2.
则解析式是:y=x-2.
根据题意得:
;
解得:
或
.
故P的坐标是:(
,
)或(
,-
).
(2)在y=-x-1中,令y=-3,解得:-x-1=-3,解得:x=2,则C的坐标是(2,-3).
设抛物线的解析式是:y=ax2+bx+c,
则
|
解得:
|
则函数的解析式是:y=x2-2x-3;
(3)A、C的中点是:(
| 1 |
| 2 |
| 3 |
| 2 |
∵△ACP是等腰三角形,且以AC为底边,
∴P在AC的中垂线上,
∴设AC的中垂线的解析式是:y=x+c,把(
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
则解析式是:y=x-2.
根据题意得:
|
解得:
|
|
故P的坐标是:(
3+
| ||
| 2 |
| ||
| 2 |
3-
| ||
| 2 |
| ||
| 2 |
点评:本题考查了待定系数法求函数的解析式,理解互相垂直的直线的解析式之间的关系是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
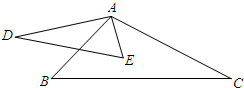 (2011•西双版纳)如图,∠DAB=∠CAE,添加一个条件:
(2011•西双版纳)如图,∠DAB=∠CAE,添加一个条件:
 (2011•西双版纳)如图,E、F是四边形ABCD的对角线BD上的两点,BF=DE,AE=CF,∠1=∠2.
(2011•西双版纳)如图,E、F是四边形ABCD的对角线BD上的两点,BF=DE,AE=CF,∠1=∠2.