题目内容
（2011•西双版纳）下列图形：它们是按一定规律排列的，依照此规律，第n个图形共有
1+3n
1+3n
_个★．分析：把五角星分成两部分，顶点处的一个不变，其它的分三条线，每一条线上后一个图形比前一个图形多一个，根据此规律找出第n个图形中五角星的个数的关系式即可；
解答：解：观察发现，第1个图形五角星的个数是，1+3=4，
第2个图形五角星的个数是，1+3×2=7，
第3个图形五角星的个数是，1+3×3=10，
第4个图形五角星的个数是，1+3×4=13，
…
依此类推，第n个图形五角星的个数是，1+3×n=1+3n；
故答案为：1+3n．
第2个图形五角星的个数是，1+3×2=7，
第3个图形五角星的个数是，1+3×3=10，
第4个图形五角星的个数是，1+3×4=13，
…
依此类推，第n个图形五角星的个数是，1+3×n=1+3n；
故答案为：1+3n．
点评：本题考查了图形变化规律的问题，把五角星分成两部分进行考虑，并找出第n个图形五角星的个数的表达式是解题的关键．
练习册系列答案
相关题目
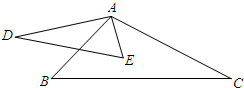（2011•西双版纳）如图，∠DAB=∠CAE，添加一个条件：
（2011•西双版纳）如图，E、F是四边形ABCD的对角线BD上的两点，BF=DE，AE=CF，∠1=∠2．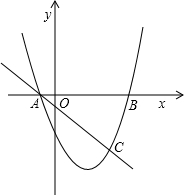
（2011•西双版纳）如图，抛物线与x轴交于A、B两点，直线y=kx-1与抛物线交于A、C两点，其中A（-1，0），B（3，0），点C的纵坐标为-3．