Question

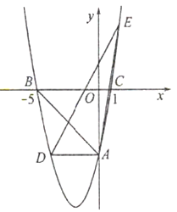
【题目】如图，在平面直角坐标系中，抛物线交轴于点，交轴于点和点，过点作轴交抛物线于点.

（1）求此抛物线的表达式；

（2）点是抛物线上一点，且点关于轴的对称点在直线上，求的面积；

（3）若点是直线下方的抛物线上一动点，当点运动到某一位置时，的面积最大，求出此时点的坐标和的最大面积.

Answer 1

【答案】（1）y=x2+4x-5；（2）20；（3）点P的坐标是（，-）时，△ABP的面积最大，此时△ABP的面积是．

【解析】（1）用待定系数法求出二次函数的解析式即可.

（2）根据点E的纵坐标是5，求出点E到AD的距离是10，求出点D的坐标，计算出的长度，即可求出的面积；

（3）设点P的坐标为（p，p2+4p-5），用待定系数法求出直线AB的解析式，列出关于△ABP的面积的式子，根据二次函数的性质即可求出面积的最大值.

（1）∵抛物线交y轴于点A，交x轴于点B（-5，0）和点C（1，0），
∴，得，
∴此抛物线的表达式是y=x2+4x-5；
（2）∵抛物线y=x2+4x-5交y轴于点A，
∴点A的坐标为（0，-5），
∵AD∥x轴，点E是抛物线上一点，且点E关于x轴的对称点在直线AD上，
∴点E的纵坐标是5，点E到AD的距离是10，
当y=-5时，-5=x2+4x-5，得x=0或x=-4，
∴点D的坐标为（-4，-5），
∴AD=4，
∴△EAD的面积是：=20；
（3）设点P的坐标为（p，p2+4p-5），如图所示，

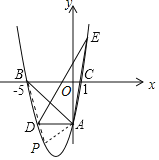
设过点A（0，-5），点B（-5，0）的直线AB的函数解析式为y=mx+n，
，得，
即直线AB的函数解析式为
当时，
∵OB=5，
∴△ABP的面积是：S= ，
∵点是直线下方的抛物线上一动点，
∴-5＜＜0，
∴当=-时，取得最大值，此时S=，点p的坐标是（，-），
即点p的坐标是（，-）时，△ABP的面积最大，此时△ABP的面积是．