��Ŀ����
����Ŀ����ͼ��������l��y= ![]() ��x��h��2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ���������ߦ���x���·��������ᷭ�ۣ�x���Ϸ���ͼ�ֲ��䣬������˺�����ͼ��
��x��h��2��2��x�ύ��A��B���㣨��A�ڵ�B����ࣩ���������ߦ���x���·��������ᷭ�ۣ�x���Ϸ���ͼ�ֲ��䣬������˺�����ͼ��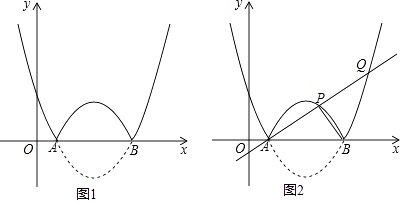
��1������A��������1��0����
����������l�ı���ʽ����ֱ��д����xΪ��ֵʱ��������ֵy��x�����������
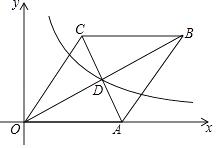
����ͼ2������A���ֱ�߽�������ͼ������������P��Q����S��ABQ=2S��ABP �� ���P�����ꣻ
��2����2��x��3ʱ��������f��ֵ��x�����������ֱ��д��h��ȡֵ��Χ��
���𰸡�
��1���⣺�ٰ�A��1��0������������y= ![]() ��x��h��2��2�еã�
��x��h��2��2�еã�
![]() ��x��h��2��2=0��
��x��h��2��2=0��
��ã�h=3��h=��1��
�ߵ�A�ڵ�B����࣬
��h��0��
��h=3��
��������l�ı���ʽΪ��y= ![]() ��x��3��2��2��
��x��3��2��2��
�������ߵĶԳ����ǣ�ֱ��x=3��
�ɶԳ��Եã�B��5��0����
��ͼ���֪����1��x��3��x��5ʱ��������ֵy��x�����������
����ͼ2����PD��x���ڵ�D���ӳ�PD��������l�ڵ�F����QE��x����E����PD��QE��
�ɶԳ��Եã�DF=PD��
��S��ABQ=2S��ABP��
�� ![]() ABQE=2��
ABQE=2�� ![]() ABPD��
ABPD��
��QE=2PD��
��PD��QE��
���PAD�ס�QAE��
�� ![]() ��
��
��AE=2AD��
��AD=a����OD=1+a��OE=1+2a��P��1+a����[ ![]() ��1+a��3��2��2]����
��1+a��3��2��2]����
�ߵ�F��Q��������l�ϣ�
��PD=DF=��[ ![]() ��1+a��3��2��2]��
��1+a��3��2��2]��
QE= ![]() ��1+2a��3��2��2��
��1+2a��3��2��2��
�� ![]() ��1+2a��3��2��2=��2[
��1+2a��3��2��2=��2[ ![]() ��1+a��3��2��2]��
��1+a��3��2��2]��
��ã�a= ![]() ��a=0���ᣩ��
��a=0���ᣩ��
��P�� ![]() ��
�� ![]() ��
��
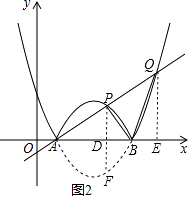
��2���⣺��y=0ʱ�� ![]() ��x��h��2��2=0��
��x��h��2��2=0��
��ã�x=h+2��h��2��
�ߵ�A�ڵ�B����࣬��h��0��
��A��h��2��0����B��h+2��0����
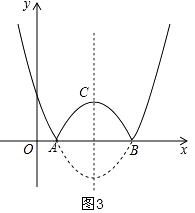
��ͼ3���������ߵĶԳ��ύ�������ڵ�C��
�����������
����ͼ���֪��ͼ��f��AC��ʱ������f��ֵ��x�����������
�� ![]() ��
��
��3��h��4��
����ͼ���֪��ͼ��f��B���Ҳ�ʱ������f��ֵ��x�����������
����h+2��2��
h��0��
������������3��h��4��h��0ʱ������f��ֵ��x�����������
����������1�������ô���ϵ�����������ߵĽ���ʽ���ɶԳ������B�����꣬����ͼ��д��������ֵy��x��������������������ƣ���x��ȡֵ������ͼ2���������ߣ������ԳƵ�F��ֱ�ǽ�������AQE������S��ABQ=2S��ABP����QE=2PD��֤����PAD�ס�QAE���� ![]() ����AE=2AD����AD=a������QE=2FD�з��̿����a��ֵ��������P�����ꣻ��2������y=0����������x��������������꣬����ͼ���г��������ƵIJ��֣��������֣��ֱ����ۣ����в���ʽ��ʽ��ɵ�h��ȡֵ��
����AE=2AD����AD=a������QE=2FD�з��̿����a��ֵ��������P�����ꣻ��2������y=0����������x��������������꣬����ͼ���г��������ƵIJ��֣��������֣��ֱ����ۣ����в���ʽ��ʽ��ɵ�h��ȡֵ��
�����㾫�������ն��κ����������ǽ����ĸ�������Ҫ֪�������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��