题目内容
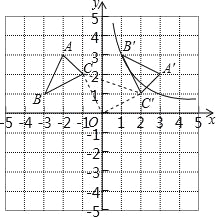
【题目】如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点三角形ABC（顶点是网格线的交点）
（1）先将△ABC竖直向上平移5个单位，再水平向右平移4个单位得到△A1B1C1，请画出△A1B1C1；
（2）将△A1B1C1绕B1点顺时针旋转90°，得△A2B1C2，请画出△A2B1C2；
（3）求线段B1C1变换到B1C2的过程中扫过区域的面积．
【答案】（1）作图见解析；（2）作图见解析；（3）
．
【解析】试题分析：（1）直接利用平移的性质得出对应点位置进而得出答案；
（2）直接利用旋转的性质进而得出对应点位置，进而得出答案；
（3）首先得出圆心角以及半径，再利用扇形面积公式直接计算得出答案．
（1）如图所示：△A1B1C1，即为所求；
（2）如图所示：△A2B1C2，即为所求；
（3）线段B1C1变换到B1C2的过程中扫过区域的面积为： 
= 
．
练习册系列答案
相关题目
【题目】八（1）班同学为了解2015年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
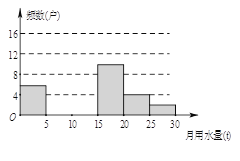
请解答以下问题：
（1）这里采用的调查方式是 （填“普查”或“抽样调查”），样本容量是 ；
（2）填空： 
， 
，并把频数分布直方图补充完整；
（3）若将月均用水量的频数绘成扇形统计图，则月均用水量“
（4）若该小区有1000户家庭，求该小区月均用水量超过10t的家庭大约有多少户？
