题目内容
【题目】如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为 . 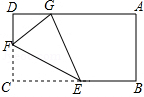
【答案】![]() ≤CF≤3
≤CF≤3
【解析】解:∵四边形ABCD是矩形, ∴∠C=90°,BC=AD=5,CD=AB=3,
当点D与F重合时,CF最大=3,如图1所示: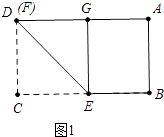
当B与E重合时,CF最小,如图2所示:
在RTABG中,∵BG=BC=5,AB=3,
∴AG= ![]() =4,
=4,
∴DG=AD﹣AG=1,设CF=FG=x,
在RT△DFG中,∵DF2+DG2=FG2 ,
∴(3﹣x)2+12=x2 ,
∴x= ![]() ,
,
∴ ![]() ≤CF≤3.
≤CF≤3.
故答案为 ![]() ≤CF≤3.
≤CF≤3.
当点E与B重合时,CF最小,先利用勾股定理求出AG,设CF=FG=x,在RT△DFG中,利用勾股定理列出方程即可解决问题,.当F与D重合时,CF最大.由此即可解决问题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目