题目内容
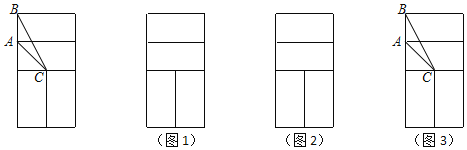
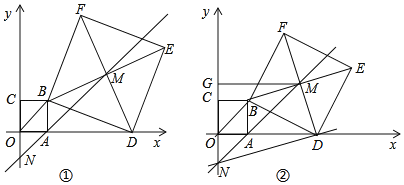
【题目】如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.
【答案】(1)详见解析;(2)详见解析;(3)N点的坐标为(0,﹣1);(4)D点坐标为(3,0).
【解析】
试题(1)根据题中给出的损矩形的定义,从图找出只有一组对角是直角的四边形即可;
(2)证明四边形BADM四个顶点到BD的中点距离相等即可;
(3)利用同弧所对的圆周角相等可得∠MAD=∠MBD,进而得到OA=ON,即可求得点N的坐标;
(4)根据正方形的性质及损矩形含有的直角,利用勾股定理求解.
(1)四边形ABMD为损矩形;
(2)取BD中点H,连结MH,AH
∵四边形OABC,BDEF是正方形
∴△ABD,△BDM都是直角三角形
∴HA=![]() BD HM=
BD HM=![]() BD
BD
∴HA=HB=HM=HD=![]() BD
BD
∴损矩形ABMD一定有外接圆
(3)∵损矩形ABMD一定有外接圆⊙H
∴![]() MAD =
MAD =![]() MBD
MBD
∵四边形BDEF是正方形
∴![]() MBD=45°
MBD=45°
∴![]() MAD=45°
MAD=45°
∴![]() OAN=45°
OAN=45°
∵OA=1
∴ON=1
∴N点的坐标为(0,-1)
(4) 延长AB交MG于点P,过点M作MQ⊥![]() 轴于点Q
轴于点Q
设MG=![]() ,则四边形APMQ为正方形
,则四边形APMQ为正方形
∴PM=AQ=![]() -1 ∴OG=MQ=
-1 ∴OG=MQ=![]() -1
-1
∵△MBP≌△MDQ
∴DQ=BP=CG=![]() -2
-2
∴MN2![]()
ND2![]()
MD2![]()
∵四边形DMGN为损矩形
∴![]()
![]()
![]()
∴![]()
∴![]() =2.5或
=2.5或![]() =1(舍去)
=1(舍去)
∴OD=3
∴D点坐标为(3,0).

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案