题目内容
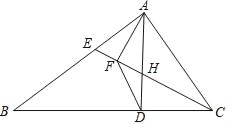
【题目】如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD平分∠ABC,DE⊥AB,AE=6,cos A=![]() .求:
.求:
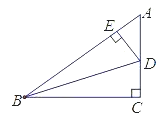
(1)DE,CD的长;(2)tan∠DBC的值.
【答案】(1)DE=8,CD=8;(2)![]() .
.
【解析】
试题1)由DE⊥AB,AE=6,cosA=![]() ,可求出AD的长,根据勾股定理可求出DE的长,由角平分线的性质可得DC=DE=8;
,可求出AD的长,根据勾股定理可求出DE的长,由角平分线的性质可得DC=DE=8;
(2)由AD=10,DC=8,得AC=AD+DC=18.由∠A=∠A,∠AED=∠ACB,可知△ADE∽△ABC,由相似三角形边长的比可求出BC的长,根据三角函数的定义可求出tan∠DBC=![]() .
.
试题解析:(1)在Rt△ADE中,由AE=6,cosA=![]() ,得:AD=10,
,得:AD=10,
由勾股定理得DE=![]() =8
=8
∵BD平分∠ABC,DE⊥AB,∠C=90°,
根据角平分线性质得:DC=DE=8.
(2)由(1)AD=10,DC=8,得:AC=AD+DC=18.
在△ADE与△ABC,∠A=∠A,∠AED=∠ACB,
∴△ADE∽△ABC得:![]() ,即
,即![]() ,BC=24,
,BC=24,
得:tan∠DBC=![]()

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案【题目】为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根调查结果绘制成的统计图(部分)如图所示.
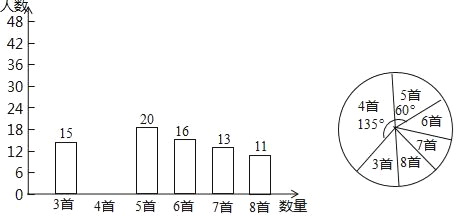
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 10 | 10 | 15 | 40 | 25 | 20 |
请根据调查的信息
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.