Question

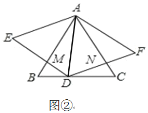
【题目】已知一次函数y=kx+b与反比例函数y= 交于A（﹣1，2），B（2，n），与y轴交于C点．
（1）求反比例函数和一次函数解析式；
（2）如图1，若将y=kx+b向下平移，使平移后的直线与y轴交于F点，与双曲线交于D，E两点，若S△ABD=3，
求D，E的坐标．

（3）如图2，P为直线y=2上的一个动点，过点P作PQ∥y轴交直线AB于Q，交双曲线于R，若QR=2QP，求P点坐标．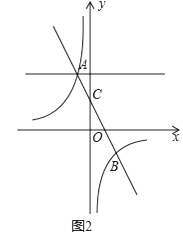

Answer 1

【答案】
（1）解：点A（﹣1，2）在反比例函数y= 的图象上，

∴m=（﹣1）×2=﹣2，

∴反比例函数的表达式为y=﹣ ，

∵点B（2，n）也在反比例函数的y=﹣ 图象上，

∴n=﹣1，

即B（2，﹣1）

把点A（﹣1，2），点B（2，﹣1）代入一次函数y=kx+b中，得 ，

解得：k=﹣1，b=1，

∴一次函数的表达式为y=﹣x+1，

答：反比例函数的表达式是y=﹣ ，一次函数的表达式是y=﹣x+1；

（2）解：如图1，

连接AF，BF，

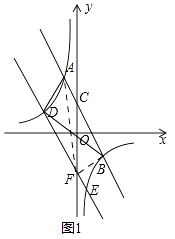
∵DE∥AB，

∴S△ABF=S△ABD=3（同底等高的两三角形面积相等），

∵直线AB的解析式为y=﹣x+1，

∴C（0，1），

设点F（0，m），

∴AF=1﹣m，

∴S△ABF=S△ACF+S△BCF= CF×|xA|+ CF×|xB|= （1﹣m）×（1+2）=3，

∴m=﹣1，

∴F（0，﹣1），

∵直线DE的解析式为y=﹣x+1，且DE∥AB，

∴直线DE的解析式为y=﹣x﹣1①．

∵反比例函数的表达式为y=﹣ ②，

联立①②解得， 或

∴D（﹣2，1），E（1，﹣2）；

（3）解：如图2

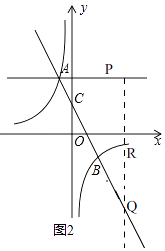
由（1）知，直线AB的解析式为y=﹣x﹣1，双曲线的解析式为y=﹣ ，

设点P（p，2），

∴Q（p，﹣p﹣1），R（p，﹣ ），

PQ=|2+p+1|，QR=|﹣p﹣1+ |，

∵QR=2QP，

∴|﹣p﹣1+ |=2|2+p+1|，

解得，p= 或p= ，

∴P（ ，2）或（ ，2）或（ ，2）或（ ，2）．

【解析】（1）把A的坐标代入反比例函数的解析式可求得m的值，从而可得到反比例函数的解析式；把点A和点B的坐标代入一次函数的解析式可求得一次函数的解析式；
（2）依据同底等高的两个三角形的面积相等可得到S△ABF=S△ABD=3，再利用三角形的面积公式可求得点F的坐标，即可得出直线DE的解析式，即可求出交点坐标；
（3）设点P（p，2），则Q（p，﹣p﹣1），R（p，﹣ ），然后可表示出PQ与QR的长度，最后依据QR=2QP，可得到关于p的方程，从而可求得p的值，从而可得到点P的坐标.